Class 12 Exam > Class 12 Questions > Difference between permutation and combinatio...
Start Learning for Free
Difference between permutation and combination?
Verified Answer
Difference between permutation and combination?
 This question is part of UPSC exam. View all Class 12 courses
This question is part of UPSC exam. View all Class 12 courses
Most Upvoted Answer
Difference between permutation and combination?
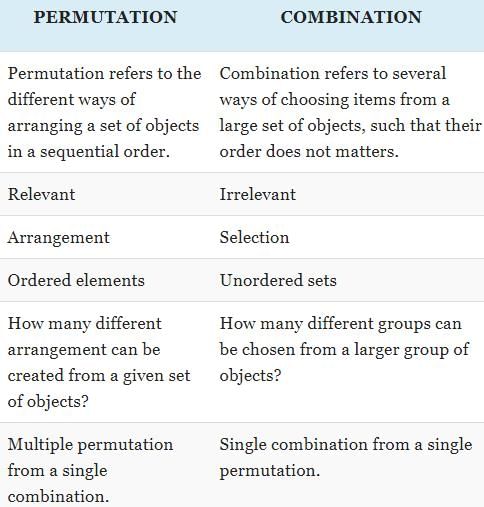
Permutation and Combination:
Permutation and combination are fundamental concepts in combinatorial mathematics that deal with different ways of arranging or selecting objects from a given set. While both involve counting and arranging elements, they have distinct characteristics and are used in different scenarios.
Permutation:
Permutation refers to the arrangement of objects or elements in a specific order. It focuses on the order or sequence in which the elements are arranged. The number of permutations can vary based on the number of objects and the length of the arrangement.
Key Points:
- Permutations are concerned with the order or arrangement of elements.
- The number of permutations can vary depending on the length of the arrangement.
- Permutations are denoted using the symbol "P" and represented as nPr, where n represents the total number of objects and r represents the number of objects to be arranged.
Example:
Consider a set of three objects: A, B, and C. The possible permutations of these objects are ABC, ACB, BAC, BCA, CAB, and CBA. Notice that the order of the objects is important in permutations.
Combination:
Combination refers to the selection of objects from a given set without considering the order or arrangement. It focuses on the selection itself rather than the order in which the elements are chosen. The number of combinations can vary based on the number of objects and the selection size.
Key Points:
- Combinations are concerned with the selection of elements without considering the order.
- The number of combinations can vary depending on the selection size.
- Combinations are denoted using the symbol "C" and represented as nCr, where n represents the total number of objects and r represents the number of objects to be selected.
Example:
Consider the same set of three objects: A, B, and C. The possible combinations of these objects are AB, AC, and BC. Notice that the order of the objects is not considered in combinations.
Summary:
In summary, permutation deals with the arrangement or order of elements, while combination focuses on the selection of elements without considering the order. Permutations are concerned with the distinct order of objects, while combinations are concerned with selecting objects without regard to their order. Understanding the difference between permutation and combination is essential in various fields, such as probability, statistics, and problem-solving.
Permutation and combination are fundamental concepts in combinatorial mathematics that deal with different ways of arranging or selecting objects from a given set. While both involve counting and arranging elements, they have distinct characteristics and are used in different scenarios.
Permutation:
Permutation refers to the arrangement of objects or elements in a specific order. It focuses on the order or sequence in which the elements are arranged. The number of permutations can vary based on the number of objects and the length of the arrangement.
Key Points:
- Permutations are concerned with the order or arrangement of elements.
- The number of permutations can vary depending on the length of the arrangement.
- Permutations are denoted using the symbol "P" and represented as nPr, where n represents the total number of objects and r represents the number of objects to be arranged.
Example:
Consider a set of three objects: A, B, and C. The possible permutations of these objects are ABC, ACB, BAC, BCA, CAB, and CBA. Notice that the order of the objects is important in permutations.
Combination:
Combination refers to the selection of objects from a given set without considering the order or arrangement. It focuses on the selection itself rather than the order in which the elements are chosen. The number of combinations can vary based on the number of objects and the selection size.
Key Points:
- Combinations are concerned with the selection of elements without considering the order.
- The number of combinations can vary depending on the selection size.
- Combinations are denoted using the symbol "C" and represented as nCr, where n represents the total number of objects and r represents the number of objects to be selected.
Example:
Consider the same set of three objects: A, B, and C. The possible combinations of these objects are AB, AC, and BC. Notice that the order of the objects is not considered in combinations.
Summary:
In summary, permutation deals with the arrangement or order of elements, while combination focuses on the selection of elements without considering the order. Permutations are concerned with the distinct order of objects, while combinations are concerned with selecting objects without regard to their order. Understanding the difference between permutation and combination is essential in various fields, such as probability, statistics, and problem-solving.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
Difference between permutation and combination?
Question Description
Difference between permutation and combination? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Difference between permutation and combination? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Difference between permutation and combination?.
Difference between permutation and combination? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Difference between permutation and combination? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Difference between permutation and combination?.
Solutions for Difference between permutation and combination? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Difference between permutation and combination? defined & explained in the simplest way possible. Besides giving the explanation of
Difference between permutation and combination?, a detailed solution for Difference between permutation and combination? has been provided alongside types of Difference between permutation and combination? theory, EduRev gives you an
ample number of questions to practice Difference between permutation and combination? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















