B Com Exam > B Com Questions > Is -1/127 any term of the series 4,-2,1,. of ...
Start Learning for Free
Is -1/127 any term of the series 4,-2,1,. of G.P?
Most Upvoted Answer
Is -1/127 any term of the series 4,-2,1,. of G.P?
Is -1/127 any term of the series 4,-2,1,. of G.P?
Introduction
The question asks whether -1/127 is any term of the series 4,-2,1,. of G.P. In order to answer this question, we need to first understand what a G.P. is and how to find its terms.
G.P. Series
A G.P. or geometric progression is a series of numbers where each term is found by multiplying the previous term by a constant ratio. The formula for finding the nth term of a G.P. is given by: a_n = a_1 * r^(n-1), where a_1 is the first term, r is the common ratio, and n is the term number.
Finding the Terms of the Series
Using the formula for finding the nth term of a G.P., we can find the terms of the series 4,-2,1,. The first term is 4 and the common ratio can be found by dividing any term by the previous term. In this case, we can divide -2 by 4 to get -1/2 as the common ratio.
Therefore, the nth term of the series is given by: a_n = 4 * (-1/2)^(n-1)
Checking if -1/127 is a Term
Now that we have the formula for finding the nth term of the series, we can check whether -1/127 is a term. We can do this by solving the formula for n and seeing if we get a whole number.
-1/127 = 4 * (-1/2)^(n-1)
Dividing both sides by 4, we get:
-1/508 = (-1/2)^(n-1)
Taking the logarithm of both sides, we get:
log(-1/508) = (n-1) * log(-1/2)
Solving for n, we get:
n = 1 - (log(-1/508) / log(-1/2))
However, we cannot take the logarithm of a negative number, so -1/127 is not a term of the series 4,-2,1,. of G.P.
Conclusion
In conclusion, -1/127 is not a term of the series 4,-2,1,. of G.P. We were able to determine this by finding the formula for the nth term of the series and solving for n using the given value of -1/127.
Community Answer
Is -1/127 any term of the series 4,-2,1,. of G.P?
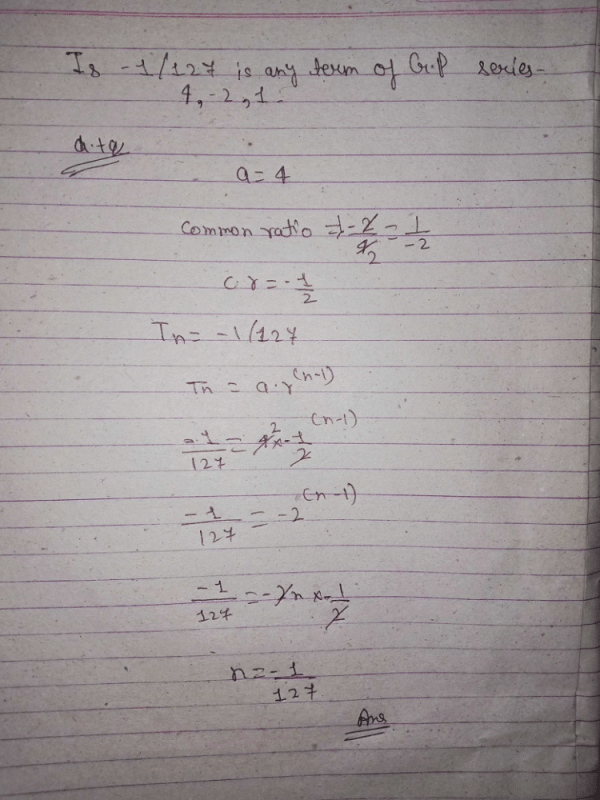

|
Explore Courses for B Com exam
|

|
Similar B Com Doubts
Is -1/127 any term of the series 4,-2,1,. of G.P?
Question Description
Is -1/127 any term of the series 4,-2,1,. of G.P? for B Com 2025 is part of B Com preparation. The Question and answers have been prepared according to the B Com exam syllabus. Information about Is -1/127 any term of the series 4,-2,1,. of G.P? covers all topics & solutions for B Com 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Is -1/127 any term of the series 4,-2,1,. of G.P?.
Is -1/127 any term of the series 4,-2,1,. of G.P? for B Com 2025 is part of B Com preparation. The Question and answers have been prepared according to the B Com exam syllabus. Information about Is -1/127 any term of the series 4,-2,1,. of G.P? covers all topics & solutions for B Com 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Is -1/127 any term of the series 4,-2,1,. of G.P?.
Solutions for Is -1/127 any term of the series 4,-2,1,. of G.P? in English & in Hindi are available as part of our courses for B Com.
Download more important topics, notes, lectures and mock test series for B Com Exam by signing up for free.
Here you can find the meaning of Is -1/127 any term of the series 4,-2,1,. of G.P? defined & explained in the simplest way possible. Besides giving the explanation of
Is -1/127 any term of the series 4,-2,1,. of G.P?, a detailed solution for Is -1/127 any term of the series 4,-2,1,. of G.P? has been provided alongside types of Is -1/127 any term of the series 4,-2,1,. of G.P? theory, EduRev gives you an
ample number of questions to practice Is -1/127 any term of the series 4,-2,1,. of G.P? tests, examples and also practice B Com tests.

|
Explore Courses for B Com exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















