JEE Exam > JEE Questions > Two mutually perpendicular long straight cond...
Start Learning for Free
Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a?
Verified Answer
Two mutually perpendicular long straight conductors carrying uniformly...
Let us make two - dimensional view of the situation. Beacuase of symmetry we can say the force on wire 2
will be the along the negative y-direction.
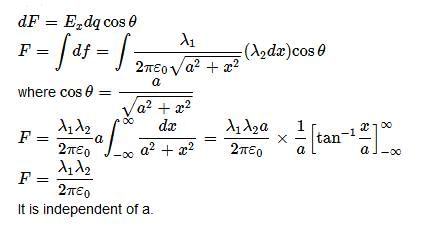
 This question is part of UPSC exam. View all JEE courses
This question is part of UPSC exam. View all JEE courses
Most Upvoted Answer
Two mutually perpendicular long straight conductors carrying uniformly...
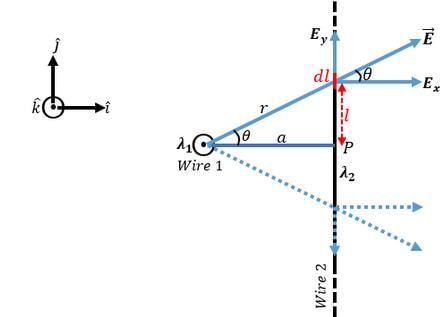
Let us name the wire having charge density
, the wire 1 and the other having charge density
, wire 2. Wire 1 is placed along z-axis i.e. normal to the screen while wire 2 is along y-axis.
We have from the triangle having its sides as a, l and r
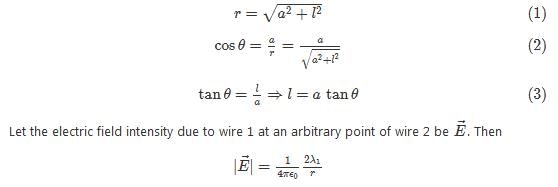
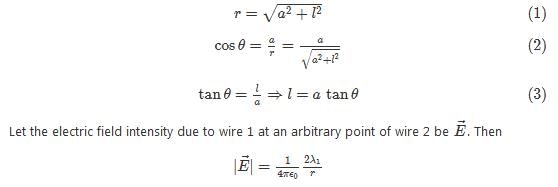
This can be resolved into x- and y-component. It is clear from the diagram that the y-component of this field is cancelled out due to the y-component of the field at a point same distance away on the other side of the point P (P is the point where the common perpendicular meets the wire 2). Thus for the whole wire 2, all the y-components are cancelled out whereas the x-components add up (see the x- and y-components shown by the dashed arrows in the diagram.


It is interesting to note that the force is independent of the distance between the wires.
While arriving at the result, it is assumed that the uniform charge distribution remains unchanged due to the field of one wire acting on the charge on the other wire. If this is not the case, the y-components of the field (see diagram) will cause charge to flow towards the ends of the wires and things will be complicated.
Community Answer
Two mutually perpendicular long straight conductors carrying uniformly...
Interaction between Perpendicular Conductors
- When two perpendicular conductors carrying charges are placed at a distance a from each other, the interaction between them depends on this distance a.
Effect of Distance a
- As the distance a between the conductors increases, the interaction between them decreases.
- This is because the electric field produced by one conductor at the location of the other conductor decreases with increasing distance.
- The force between the conductors is directly proportional to the product of their linear charge densities and inversely proportional to the square of the distance between them.
Mathematical Representation
- The interaction between the conductors can be mathematically expressed as F = k * a1 * a2 / a^2, where F is the force between the conductors, k is the electrostatic constant, a1 and a2 are the linear charge densities of the conductors, and a is the distance between them.
Conclusion
- In conclusion, the interaction between two perpendicular conductors carrying charges depends on the distance between them. As the distance increases, the force between the conductors decreases. This relationship is governed by Coulomb's law and the principles of electrostatics.
- When two perpendicular conductors carrying charges are placed at a distance a from each other, the interaction between them depends on this distance a.
Effect of Distance a
- As the distance a between the conductors increases, the interaction between them decreases.
- This is because the electric field produced by one conductor at the location of the other conductor decreases with increasing distance.
- The force between the conductors is directly proportional to the product of their linear charge densities and inversely proportional to the square of the distance between them.
Mathematical Representation
- The interaction between the conductors can be mathematically expressed as F = k * a1 * a2 / a^2, where F is the force between the conductors, k is the electrostatic constant, a1 and a2 are the linear charge densities of the conductors, and a is the distance between them.
Conclusion
- In conclusion, the interaction between two perpendicular conductors carrying charges depends on the distance between them. As the distance increases, the force between the conductors decreases. This relationship is governed by Coulomb's law and the principles of electrostatics.
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.

|
Explore Courses for JEE exam
|

|
Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a?
Question Description
Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a?.
Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a?.
Solutions for Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a? defined & explained in the simplest way possible. Besides giving the explanation of
Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a?, a detailed solution for Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a? has been provided alongside types of Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a? theory, EduRev gives you an
ample number of questions to practice Two mutually perpendicular long straight conductors carrying uniformly disrtibuted charged of linear charge densities a1 and a2 are positions at a distance a from each othet. How does the interaction between the rods depends on a? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























