All Courses
Explore Courses UPSC Exam UPSC Test Series Free Notes EduRev Infinity Get the App Login Join for Free
Sign in Open App
JEE Exam  >  JEE Questions  >  In the decomposition of H2 O2 at 300 Kelvin t... Start Learning for Free
SaveJoin the Discussion on the App
In the decomposition of H2 O2 at 300 Kelvin the energy of activation was found to be 18 kcal per mole while it decrease 6 KCL per mole when the decomposition was carried out in the presence of a catalyse at 300 Kelvin how many time is the catalysed reaction faster than the uncatalysed one ?
Clear all your JEE doubts with EduRev
Verified Answer
In the decomposition of H2 O2 at 300 Kelvin the energy of activation w...
Ans.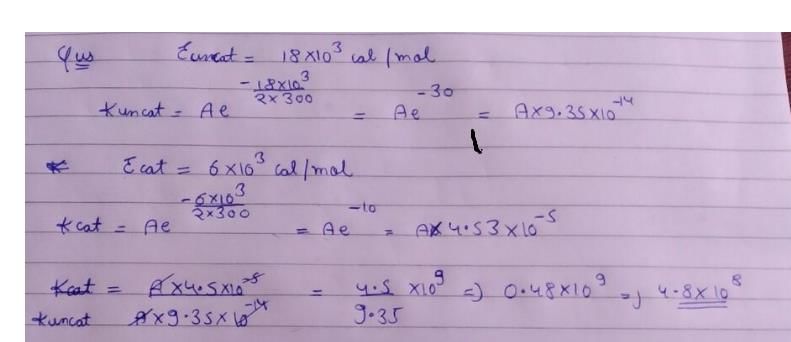
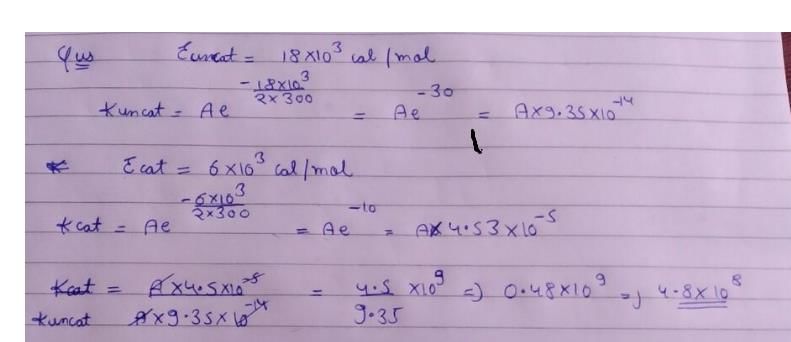
This question is part of UPSC exam. View all JEE courses
Most Upvoted Answer
In the decomposition of H2 O2 at 300 Kelvin the energy of activation w...
Calculation of Reaction Rate:
- The rate constant for the uncatalyzed reaction can be calculated using the Arrhenius equation: k = Ae^(-Ea/RT), where Ea is the activation energy, R is the gas constant, T is the temperature in Kelvin, and A is the pre-exponential factor.
- For the uncatalyzed reaction: k_uncatalyzed = A * e^(-18,000 cal/mol / (1.987 cal/mol*K * 300 K)) = A * e^(-18,000 cal/mol / 596.1 cal/mol) = A * e^(-30.2)
- For the catalyzed reaction: k_catalyzed = A * e^(-12,000 cal/mol / (1.987 cal/mol*K * 300 K)) = A * e^(-12,000 cal/mol / 596.1 cal/mol) = A * e^(-20.1)

Comparison of Reaction Rates:
- The ratio of the catalyzed rate constant to the uncatalyzed rate constant can be calculated: k_catalyzed / k_uncatalyzed = (A * e^(-20.1)) / (A * e^(-30.2)) = e^(10.1)
- Therefore, the catalyzed reaction is e^(10.1) times faster than the uncatalyzed reaction.
- This means that the presence of the catalyst increases the reaction rate by a factor of approximately 22,026.

Explanation:
- The decrease in activation energy from 18 kcal/mol to 12 kcal/mol in the presence of the catalyst lowers the energy barrier for the reaction to occur.
- This allows more reactant molecules to overcome the activation energy barrier and participate in the reaction, leading to a significant increase in the reaction rate.
- The catalyst provides an alternative reaction pathway with a lower activation energy, thereby accelerating the rate of the reaction.
- Overall, the catalyzed reaction proceeds much faster than the uncatalyzed reaction due to the lower energy barrier provided by the catalyst.
Explore Courses for JEE exam

Similar JEE Doubts

There are many reactions which obey a first order rate equation although it reality they are bi- or ter-molecular. As an example of these may be taken the decomposition of Carbonyl sulfide in water, namely, COS + H20 002 + H2SAccording to the law of mass action this reaction should be second order with the rate dependent on the concentration of both the carbonyl sulfide and the water. Actually however, the rate is found to be first order with respect to the carbonyl sulfide and independent of the water Reactions exhibiting such behaviour are said to be pseudo-molecular.The pseudo-unimoecuar nature of this reaction is explainable by the fact that water is present in such excess that its concentration remains practically constant during the course of the reaction. Under these condition b x = b, and the rate equation becomesOn integration this leads towhich is the equation for a first order reaction. It is evident, however, that the now constant k is not independent of the concentration, as is the case with true first order constants, but may vary with b if the latter is changed appreciably, When such is the case, the true constant k2 can be obtained from k by dividing the latter by b. pseudo-molecular reactions are encountered whenever one or more of the reactants remain constants during the course of an experiment. This is the case with reactions conducted in solvents which are themselves one of the reactants, as in the decomposition of carbonyl sulfide in water, or in the esterification of acetic anhydride in alcohol(CH3C0)20 + 2C2H5OH 2CH3C00C2H5 + H20Again, this is also true of reactions subject to catalysis, in which case the concentration of the catalyst does not change. The decomposition of diacetone alcohol to acetone in aqueous solution is catalysed by hydroxyl ions, with the rate proportional to the concentration of the alcohol and that of the base. Since the concentration of the base does not change within any one experiment, however, the rate equation reduces to one of first order with respect to the alcohol. But the rateconstant k obtained for various concentrations of base are not identical, as may be seen from table. To obtain from these the true second order velocity constant, the ks must be divided by the hydroxyl ion concentration. When this is done excellent k2 values result, as column 3 indicatesTable : Decomposition of diacetone alcohol in water at 25C (Catalyst : NaOH)Q.By what factor does the rate of reaction of diacetone alcohol in water solution change if p0H is increased by 2 units other things remaining same ?

Top Courses for JEEView all

Top Courses for JEE

In the decomposition of H2 O2 at 300 Kelvin the energy of activation was found to be 18 kcal per mole while it decrease 6 KCL per mole when the decomposition was carried out in the presence of a catalyse at 300 Kelvin how many time is the catalysed reaction faster than the uncatalysed one ?
Question Description
In the decomposition of H2 O2 at 300 Kelvin the energy of activation was found to be 18 kcal per mole while it decrease 6 KCL per mole when the decomposition was carried out in the presence of a catalyse at 300 Kelvin how many time is the catalysed reaction faster than the uncatalysed one ? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about In the decomposition of H2 O2 at 300 Kelvin the energy of activation was found to be 18 kcal per mole while it decrease 6 KCL per mole when the decomposition was carried out in the presence of a catalyse at 300 Kelvin how many time is the catalysed reaction faster than the uncatalysed one ? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In the decomposition of H2 O2 at 300 Kelvin the energy of activation was found to be 18 kcal per mole while it decrease 6 KCL per mole when the decomposition was carried out in the presence of a catalyse at 300 Kelvin how many time is the catalysed reaction faster than the uncatalysed one ?.
Solutions for In the decomposition of H2 O2 at 300 Kelvin the energy of activation was found to be 18 kcal per mole while it decrease 6 KCL per mole when the decomposition was carried out in the presence of a catalyse at 300 Kelvin how many time is the catalysed reaction faster than the uncatalysed one ? in English & in Hindi are available as part of our courses for JEE. Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of In the decomposition of H2 O2 at 300 Kelvin the energy of activation was found to be 18 kcal per mole while it decrease 6 KCL per mole when the decomposition was carried out in the presence of a catalyse at 300 Kelvin how many time is the catalysed reaction faster than the uncatalysed one ? defined & explained in the simplest way possible. Besides giving the explanation of In the decomposition of H2 O2 at 300 Kelvin the energy of activation was found to be 18 kcal per mole while it decrease 6 KCL per mole when the decomposition was carried out in the presence of a catalyse at 300 Kelvin how many time is the catalysed reaction faster than the uncatalysed one ?, a detailed solution for In the decomposition of H2 O2 at 300 Kelvin the energy of activation was found to be 18 kcal per mole while it decrease 6 KCL per mole when the decomposition was carried out in the presence of a catalyse at 300 Kelvin how many time is the catalysed reaction faster than the uncatalysed one ? has been provided alongside types of In the decomposition of H2 O2 at 300 Kelvin the energy of activation was found to be 18 kcal per mole while it decrease 6 KCL per mole when the decomposition was carried out in the presence of a catalyse at 300 Kelvin how many time is the catalysed reaction faster than the uncatalysed one ? theory, EduRev gives you an ample number of questions to practice In the decomposition of H2 O2 at 300 Kelvin the energy of activation was found to be 18 kcal per mole while it decrease 6 KCL per mole when the decomposition was carried out in the presence of a catalyse at 300 Kelvin how many time is the catalysed reaction faster than the uncatalysed one ? tests, examples and also practice JEE tests.
Explore Courses for JEE exam

Top Courses for JEE

Explore Courses

Suggested Free Tests

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Get App
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup