Class 12 Exam > Class 12 Questions > Angle of polarization for air to water medium...
Start Learning for Free
Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.?
Most Upvoted Answer
Angle of polarization for air to water medium is 53 degree. Find the r...
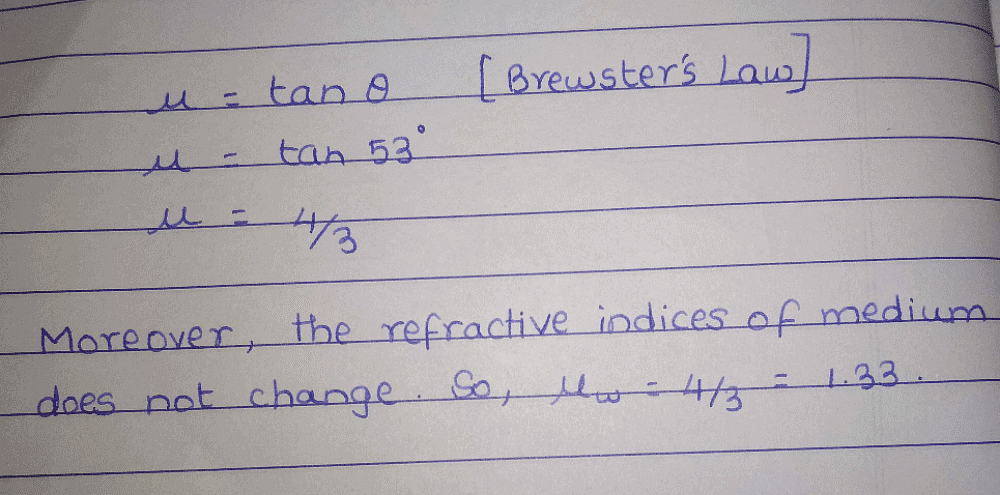
Community Answer
Angle of polarization for air to water medium is 53 degree. Find the r...
Understanding the Angle of Polarization
The angle of polarization (also known as Brewster's angle) is the angle at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection. This phenomenon occurs when the reflected and refracted rays are perpendicular to each other.
Formula for Brewster's Angle
The relationship between the angle of polarization (θ) and the refractive indices of the two media can be derived from Brewster's Law:
tan(θ) = n₂/n₁
Where:
- θ = angle of polarization (53 degrees in this case)
- n₂ = refractive index of the second medium (water)
- n₁ = refractive index of the first medium (air, approximately 1)
Calculating the Refractive Index of Water
1. **Convert Angle to Radians:**
- θ = 53 degrees = tan(53°)
2. **Using the Formula:**
- tan(53°) ≈ 1.327
- Therefore, the equation becomes:
1.327 = n₂/1
- This simplifies to:
n₂ = 1.327
3. **Conclusion:**
- The refractive index of water (n₂) is approximately 1.327.
Implications of the Refractive Index
The refractive index indicates how much light slows down and bends when entering a medium. A refractive index of 1.327 for water implies that light travels slower in water than in air, leading to a change in speed and direction of light as it transitions between these two media.
Final Note
Understanding the angle of polarization and the refractive index enhances comprehension of optical phenomena, crucial in fields like optics, photography, and material science.
The angle of polarization (also known as Brewster's angle) is the angle at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection. This phenomenon occurs when the reflected and refracted rays are perpendicular to each other.
Formula for Brewster's Angle
The relationship between the angle of polarization (θ) and the refractive indices of the two media can be derived from Brewster's Law:
tan(θ) = n₂/n₁
Where:
- θ = angle of polarization (53 degrees in this case)
- n₂ = refractive index of the second medium (water)
- n₁ = refractive index of the first medium (air, approximately 1)
Calculating the Refractive Index of Water
1. **Convert Angle to Radians:**
- θ = 53 degrees = tan(53°)
2. **Using the Formula:**
- tan(53°) ≈ 1.327
- Therefore, the equation becomes:
1.327 = n₂/1
- This simplifies to:
n₂ = 1.327
3. **Conclusion:**
- The refractive index of water (n₂) is approximately 1.327.
Implications of the Refractive Index
The refractive index indicates how much light slows down and bends when entering a medium. A refractive index of 1.327 for water implies that light travels slower in water than in air, leading to a change in speed and direction of light as it transitions between these two media.
Final Note
Understanding the angle of polarization and the refractive index enhances comprehension of optical phenomena, crucial in fields like optics, photography, and material science.

|
Explore Courses for Class 12 exam
|

|
Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.?
Question Description
Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.?.
Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.?.
Solutions for Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.? defined & explained in the simplest way possible. Besides giving the explanation of
Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.?, a detailed solution for Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.? has been provided alongside types of Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.? theory, EduRev gives you an
ample number of questions to practice Angle of polarization for air to water medium is 53 degree. Find the refractive index of water.? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

















