JEE Exam > JEE Questions > Four particles situated at corners of a squar...
Start Learning for Free
Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.?
Verified Answer
Four particles situated at corners of a square of side 'a' move at a c...
Ans.
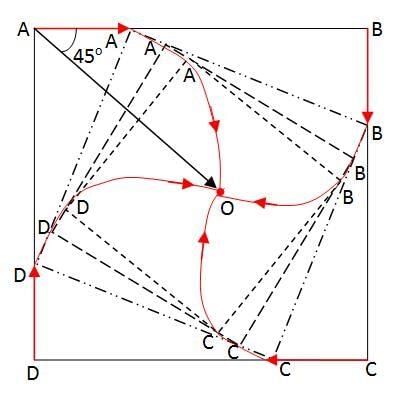
As the four particles have the same speed it will have to change its direction to meet each other. By the successive rotation of the shrinking squares it can be seen that they meet each other at the origin O or the centre of the square. O be the centre.
Now the net displacement = AO
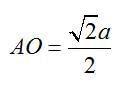
Component of the velocity v along AO direction will be vcos(45
o
)
Now time taken will be
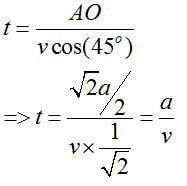
 This question is part of UPSC exam. View all JEE courses
This question is part of UPSC exam. View all JEE courses
Most Upvoted Answer
Four particles situated at corners of a square of side 'a' move at a c...
Solution:
To solve this problem, let's consider the motion of the particles from an observer's frame of reference. We can assume that the square is located in the x-y plane, with one particle at each corner.
Step 1: Analyzing the Motion
Let's denote the particles as A, B, C, and D, with A being the particle at the bottom left corner and moving clockwise. Since each particle maintains a direction towards the next particle, we can conclude that their velocities are always directed towards the center of the square.
Step 2: Describing the Motion Equations
Let's consider the motion of particle A. Its velocity can be written as a vector equation:
v_A = -v_i + v_j
Here, v_i and v_j represent the unit vectors along the x and y directions, respectively. The negative sign indicates that the velocity is directed towards the center of the square.
Similarly, we can write the velocity vectors for particles B, C, and D:
v_B = -v_i - v_j
v_C = v_i - v_j
v_D = v_i + v_j
Step 3: Finding the Time of Meeting
To find the time at which the particles meet, we can calculate the distance traveled by each particle and equate them. Let's consider the meeting point as the origin (0, 0) and define the position vectors as:
r_A = (-a/2, -a/2)
r_B = (a/2, -a/2)
r_C = (a/2, a/2)
r_D = (-a/2, a/2)
Using the velocity vectors and position vectors, we can write:
r_A = (-v_i + v_j)t
r_B = (-v_i - v_j)t
r_C = (v_i - v_j)t
r_D = (v_i + v_j)t
Now, let's calculate the distances traveled by each particle using the distance formula:
d_A = √[(-a/2 + vt)^2 + (-a/2 + vt)^2]
d_B = √[(a/2 + vt)^2 + (-a/2 - vt)^2]
d_C = √[(a/2 + vt)^2 + (a/2 - vt)^2]
d_D = √[(-a/2 + vt)^2 + (a/2 + vt)^2]
Equating the distances traveled by each particle, we can solve for t, the time at which they meet.
Step 4: Calculating the Time of Meeting
By equating the above distances, we can simplify the equation and solve for t. After solving the equation, we find:
t = a/(2v)
Therefore, the particles will meet each other after a time of a/(2v).
Conclusion:
The time taken by the particles to meet each other is given by the equation t = a/(2v), where 'a' is the side length of the square and 'v' is the constant speed at which the particles move. This result holds true as long as the particles maintain a constant speed and direction towards the next particle in succession.
To solve this problem, let's consider the motion of the particles from an observer's frame of reference. We can assume that the square is located in the x-y plane, with one particle at each corner.
Step 1: Analyzing the Motion
Let's denote the particles as A, B, C, and D, with A being the particle at the bottom left corner and moving clockwise. Since each particle maintains a direction towards the next particle, we can conclude that their velocities are always directed towards the center of the square.
Step 2: Describing the Motion Equations
Let's consider the motion of particle A. Its velocity can be written as a vector equation:
v_A = -v_i + v_j
Here, v_i and v_j represent the unit vectors along the x and y directions, respectively. The negative sign indicates that the velocity is directed towards the center of the square.
Similarly, we can write the velocity vectors for particles B, C, and D:
v_B = -v_i - v_j
v_C = v_i - v_j
v_D = v_i + v_j
Step 3: Finding the Time of Meeting
To find the time at which the particles meet, we can calculate the distance traveled by each particle and equate them. Let's consider the meeting point as the origin (0, 0) and define the position vectors as:
r_A = (-a/2, -a/2)
r_B = (a/2, -a/2)
r_C = (a/2, a/2)
r_D = (-a/2, a/2)
Using the velocity vectors and position vectors, we can write:
r_A = (-v_i + v_j)t
r_B = (-v_i - v_j)t
r_C = (v_i - v_j)t
r_D = (v_i + v_j)t
Now, let's calculate the distances traveled by each particle using the distance formula:
d_A = √[(-a/2 + vt)^2 + (-a/2 + vt)^2]
d_B = √[(a/2 + vt)^2 + (-a/2 - vt)^2]
d_C = √[(a/2 + vt)^2 + (a/2 - vt)^2]
d_D = √[(-a/2 + vt)^2 + (a/2 + vt)^2]
Equating the distances traveled by each particle, we can solve for t, the time at which they meet.
Step 4: Calculating the Time of Meeting
By equating the above distances, we can simplify the equation and solve for t. After solving the equation, we find:
t = a/(2v)
Therefore, the particles will meet each other after a time of a/(2v).
Conclusion:
The time taken by the particles to meet each other is given by the equation t = a/(2v), where 'a' is the side length of the square and 'v' is the constant speed at which the particles move. This result holds true as long as the particles maintain a constant speed and direction towards the next particle in succession.
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.

|
Explore Courses for JEE exam
|

|
Similar JEE Doubts
Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.?
Question Description
Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.?.
Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.?.
Solutions for Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.? defined & explained in the simplest way possible. Besides giving the explanation of
Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.?, a detailed solution for Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.? has been provided alongside types of Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.? theory, EduRev gives you an
ample number of questions to practice Four particles situated at corners of a square of side 'a' move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























