JEE Exam > JEE Questions > A moving coil galvanometer of resistance 100 ...
Start Learning for Free
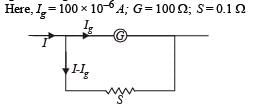
A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflection
- a)100.1 mA
- b)1000.1 mA
- c)10.01 mA
- d)1.01 mA
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
A moving coil galvanometer of resistance 100 Ω is used as an amm...
KEY CONCEPT :
IgG = (I – Ig) S
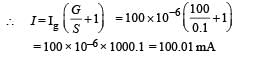
Most Upvoted Answer
A moving coil galvanometer of resistance 100 Ω is used as an amm...
Since the resistance of the galvanometer is 100 Ω, we can use Ohm's Law to find the current passing through the galvanometer.
Ohm's Law states that the current (I) flowing through a resistor is equal to the voltage (V) across the resistor divided by the resistance (R).
In this case, the voltage across the galvanometer is not given, so we cannot directly calculate the current. However, we can use the fact that a galvanometer is typically used as a current measuring device when connected in parallel with a known resistance (R). The total current passing through the parallel combination is given by the sum of the currents passing through the galvanometer and the known resistance.
Let's assume that the total current passing through the parallel combination is I_total, and the current passing through the known resistance is I_known.
Since the galvanometer and the known resistor are connected in parallel, they have the same voltage across them. Therefore, we can write the following equation:
I_total = I_galvanometer + I_known
We know that the resistance of the galvanometer is 100 Ω, so we can calculate the current passing through the known resistance using Ohm's Law:
I_known = V / R_known
where V is the voltage across the known resistance and R_known is the resistance of the known resistance.
Now, we can substitute this expression into the equation above:
I_total = I_galvanometer + (V / R_known)
We can rearrange this equation to solve for I_galvanometer:
I_galvanometer = I_total - (V / R_known)
So, to find the current passing through the galvanometer, we need to know the total current passing through the parallel combination and the voltage across the known resistance.
Ohm's Law states that the current (I) flowing through a resistor is equal to the voltage (V) across the resistor divided by the resistance (R).
In this case, the voltage across the galvanometer is not given, so we cannot directly calculate the current. However, we can use the fact that a galvanometer is typically used as a current measuring device when connected in parallel with a known resistance (R). The total current passing through the parallel combination is given by the sum of the currents passing through the galvanometer and the known resistance.
Let's assume that the total current passing through the parallel combination is I_total, and the current passing through the known resistance is I_known.
Since the galvanometer and the known resistor are connected in parallel, they have the same voltage across them. Therefore, we can write the following equation:
I_total = I_galvanometer + I_known
We know that the resistance of the galvanometer is 100 Ω, so we can calculate the current passing through the known resistance using Ohm's Law:
I_known = V / R_known
where V is the voltage across the known resistance and R_known is the resistance of the known resistance.
Now, we can substitute this expression into the equation above:
I_total = I_galvanometer + (V / R_known)
We can rearrange this equation to solve for I_galvanometer:
I_galvanometer = I_total - (V / R_known)
So, to find the current passing through the galvanometer, we need to know the total current passing through the parallel combination and the voltage across the known resistance.

|
Explore Courses for JEE exam
|

|
Similar JEE Doubts
A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer?
Question Description
A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer?.
A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer?.
Solutions for A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer?, a detailed solution for A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A moving coil galvanometer of resistance 100 Ω is used as an ammeter using a resistance 0.1 Ω. The maximum deflection current in the galvanometer is 100 μA. Find the minimum current in the circuit so that the ammeter shows maximum deflectiona)100.1 mAb)1000.1 mAc)10.01 mAd)1.01 mACorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























