Class 12 Exam > Class 12 Questions > Monochromatic radiation emitted when electron...
Start Learning for Free
Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]
- a)4 × 1015 Hz
- b)5 × 1015 Hz
- c)1.6 × 1015` Hz
- d)2.5 × 1015 Hz
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Monochromatic radiation emitted when electronon hydrogen atom jumps fr...
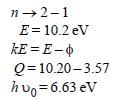
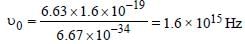
Most Upvoted Answer
Monochromatic radiation emitted when electronon hydrogen atom jumps fr...
To find the threshold frequency of the material, we need to use the formula for the stopping potential in the photoelectric effect:
V_stop = (h/λ) - (φ/e)
Where:
V_stop is the stopping potential (3.57 V in this case)
h is Planck's constant (6.626 x 10^-34 J*s)
λ is the wavelength of the monochromatic radiation emitted (which corresponds to the transition from the first excited state to the ground state of hydrogen)
φ is the work function of the material (which represents the minimum energy required to remove an electron from an atom in the material)
e is the elementary charge (1.602 x 10^-19 C)
Since we are given the wavelength, we can convert it to frequency using the equation:
c = λ * ν
Where:
c is the speed of light (3 x 10^8 m/s)
ν is the frequency
Solving for ν, we get:
ν = c / λ
Now we can substitute this expression for ν into the formula for the stopping potential:
V_stop = (h / (c / λ)) - (φ / e)
Simplifying, we get:
V_stop = (hc / λ) - (φ / e)
Since we are looking for the threshold frequency, we want the stopping potential to be zero. Therefore, we can set V_stop = 0 and solve for the threshold frequency:
0 = (hc / λ) - (φ / e)
Solving for λ, we get:
λ = (hc / (φ / e))
Now we can plug in the given values:
h = 6.626 x 10^-34 J*s
c = 3 x 10^8 m/s
φ = unknown (to be determined)
e = 1.602 x 10^-19 C
Plugging in these values, we get:
λ = (6.626 x 10^-34 J*s * 3 x 10^8 m/s) / ((φ / (1.602 x 10^-19 C))
Simplifying, we get:
λ = (19.878 x 10^-26 J*m) / (φ / 1.602 x 10^-19 C)
Now we can rearrange the equation to solve for φ:
φ = (19.878 x 10^-26 J*m) / (λ / 1.602 x 10^-19 C)
Substituting the given stopping potential of 3.57 V, we get:
φ = (19.878 x 10^-26 J*m) / (3.57 V / 1.602 x 10^-19 C)
Simplifying, we get:
φ = (19.878 x 10^-26 J*m * 1.602 x 10^-19 C) / (3.57 V)
φ = 8.913 x 10^-7 J
Now we can substitute this value for φ back into the equation for λ:
λ = (6.626 x 10^-34 J*s * 3 x 10^8 m/s) / ((8.913 x 10^-7 J) / (1.602 x 10^-19 C))
Simplifying, we get:
λ = (19.878 x 10^-26 J*m) / (8.913 x 10^-7
V_stop = (h/λ) - (φ/e)
Where:
V_stop is the stopping potential (3.57 V in this case)
h is Planck's constant (6.626 x 10^-34 J*s)
λ is the wavelength of the monochromatic radiation emitted (which corresponds to the transition from the first excited state to the ground state of hydrogen)
φ is the work function of the material (which represents the minimum energy required to remove an electron from an atom in the material)
e is the elementary charge (1.602 x 10^-19 C)
Since we are given the wavelength, we can convert it to frequency using the equation:
c = λ * ν
Where:
c is the speed of light (3 x 10^8 m/s)
ν is the frequency
Solving for ν, we get:
ν = c / λ
Now we can substitute this expression for ν into the formula for the stopping potential:
V_stop = (h / (c / λ)) - (φ / e)
Simplifying, we get:
V_stop = (hc / λ) - (φ / e)
Since we are looking for the threshold frequency, we want the stopping potential to be zero. Therefore, we can set V_stop = 0 and solve for the threshold frequency:
0 = (hc / λ) - (φ / e)
Solving for λ, we get:
λ = (hc / (φ / e))
Now we can plug in the given values:
h = 6.626 x 10^-34 J*s
c = 3 x 10^8 m/s
φ = unknown (to be determined)
e = 1.602 x 10^-19 C
Plugging in these values, we get:
λ = (6.626 x 10^-34 J*s * 3 x 10^8 m/s) / ((φ / (1.602 x 10^-19 C))
Simplifying, we get:
λ = (19.878 x 10^-26 J*m) / (φ / 1.602 x 10^-19 C)
Now we can rearrange the equation to solve for φ:
φ = (19.878 x 10^-26 J*m) / (λ / 1.602 x 10^-19 C)
Substituting the given stopping potential of 3.57 V, we get:
φ = (19.878 x 10^-26 J*m) / (3.57 V / 1.602 x 10^-19 C)
Simplifying, we get:
φ = (19.878 x 10^-26 J*m * 1.602 x 10^-19 C) / (3.57 V)
φ = 8.913 x 10^-7 J
Now we can substitute this value for φ back into the equation for λ:
λ = (6.626 x 10^-34 J*s * 3 x 10^8 m/s) / ((8.913 x 10^-7 J) / (1.602 x 10^-19 C))
Simplifying, we get:
λ = (19.878 x 10^-26 J*m) / (8.913 x 10^-7
|
Explore Courses for Class 12 exam
|
|
Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer?
Question Description
Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer?.
Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Monochromatic radiation emitted when electronon hydrogen atom jumps from first excited tothe ground state irradiates a photosensitivematerial. The stopping potential is measured tobe 3.57 V. The threshold frequency of the materialsis : [2012]a)4 × 1015 Hzb)5 × 1015 Hzc)1.6 × 1015` Hzd)2.5 × 1015 HzCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Class 12 tests.
|
|
Explore Courses for Class 12 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup