Class 12 Exam > Class 12 Questions > The ionization energy of the electron in theh...
Start Learning for Free
The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]
- a)n = 3 to n = 1 states
- b)n = 2 to n = 1 states
- c)n = 4 to n = 3 states
- d)n = 3 to n = 2 states
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
The ionization energy of the electron in thehydrogen atom in its groun...
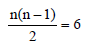

n2 – n – 12 = 0
(n – 4) (n + 3) = 0 or n = 4
(n – 4) (n + 3) = 0 or n = 4
Most Upvoted Answer
The ionization energy of the electron in thehydrogen atom in its groun...
Explanation:
When hydrogen atoms are excited to higher energy levels, they release energy in the form of photons. The energy of a photon is given by the equation:
E = hc/λ
where E is the energy of the photon, h is Planck's constant, c is the speed of light, and λ is the wavelength of the photon.
The maximum wavelength of the emitted radiation corresponds to the transition that releases the least amount of energy. This occurs when the electron transitions from a higher energy level to the ground state.
To determine which transition corresponds to the maximum wavelength of the emitted radiation, we can use the equation:
ΔE = -Rh/n^2f + Rh/n^2i
where ΔE is the energy released during the transition, Rh is the Rydberg constant (2.18 x 10^-18 J), nif is the initial energy level, and nf is the final energy level.
We want to find the transition that releases the least amount of energy, which corresponds to the maximum wavelength of the emitted radiation. This occurs when nf is as large as possible and nif is as small as possible.
Using this approach, we find that the transition between n = 4 and n = 3 states releases the least amount of energy, and therefore corresponds to the maximum wavelength of the emitted radiation. The correct answer is option C.
When hydrogen atoms are excited to higher energy levels, they release energy in the form of photons. The energy of a photon is given by the equation:
E = hc/λ
where E is the energy of the photon, h is Planck's constant, c is the speed of light, and λ is the wavelength of the photon.
The maximum wavelength of the emitted radiation corresponds to the transition that releases the least amount of energy. This occurs when the electron transitions from a higher energy level to the ground state.
To determine which transition corresponds to the maximum wavelength of the emitted radiation, we can use the equation:
ΔE = -Rh/n^2f + Rh/n^2i
where ΔE is the energy released during the transition, Rh is the Rydberg constant (2.18 x 10^-18 J), nif is the initial energy level, and nf is the final energy level.
We want to find the transition that releases the least amount of energy, which corresponds to the maximum wavelength of the emitted radiation. This occurs when nf is as large as possible and nif is as small as possible.
Using this approach, we find that the transition between n = 4 and n = 3 states releases the least amount of energy, and therefore corresponds to the maximum wavelength of the emitted radiation. The correct answer is option C.

|
Explore Courses for Class 12 exam
|

|
Question Description
The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer?.
The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer?.
Solutions for The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The ionization energy of the electron in thehydrogen atom in its ground state is 13.6 eV.The atoms are excited to higher energy levels toemit radiations of 6 wavelengths. Maximumwavelength of emitted radiation corresponds tothe transition between [2009]a)n = 3 to n = 1 statesb)n = 2 to n = 1 statesc)n = 4 to n = 3 statesd)n = 3 to n = 2 statesCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















