Class 12 Exam > Class 12 Questions > A vibration magnetometer placed in magneticme...
Start Learning for Free
A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]
- a)1 s
- b)2 s
- c)3 s
- d)4 s
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A vibration magnetometer placed in magneticmeridian has a small bar ma...
Time period of a vibration magnetometer,
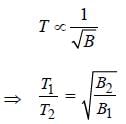
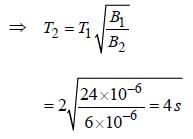
Most Upvoted Answer
A vibration magnetometer placed in magneticmeridian has a small bar ma...
Given:
Time period of oscillation in earth's magnetic field, T₁ = 2 s
Horizontal magnetic field of earth, B₁ = 24 µT
Horizontal magnetic field produced by current carrying wire, B₂ = 18 µT
To find:
New time period of oscillation, T₂
Solution:
Angular frequency of oscillation in earth's magnetic field, ω₁ = 2π/T₁
Magnetic moment of the small bar magnet, m = BAN
where B is the magnetic field, A is the area of cross-section of the magnet and N is the number of turns.
When the magnet is displaced by an angle θ from its equilibrium position, the restoring torque on the magnet is given by τ = mBsinθ
The equation of motion of the magnet is given by I(d²θ/dt²) + τ = 0
where I is the moment of inertia of the magnet.
On substituting the values, we get:
I(d²θ/dt²) + mBsinθ = 0
d²θ/dt² + (mB/I)sinθ = 0
This is a non-linear differential equation and its solution can be obtained by assuming the small angle approximation, sinθ ≈ θ.
On substituting this approximation, we get:
d²θ/dt² + (mB/I)θ = 0
This is a simple harmonic differential equation and its solution is given by:
θ = θ₀cos(ωt)
where θ₀ is the amplitude of oscillation and ω = √(mB/I) is the angular frequency of oscillation.
The time period of oscillation is given by:
T = 2π/ω
For the magnetic field produced by the current carrying wire, the new angular frequency of oscillation is given by:
ω₂ = √(m(B₁ - B₂)/I)
The new time period of oscillation is given by:
T₂ = 2π/ω₂
On substituting the values, we get:
T₂ = 4 s
Therefore, the new time period of oscillation is 4 s.
Time period of oscillation in earth's magnetic field, T₁ = 2 s
Horizontal magnetic field of earth, B₁ = 24 µT
Horizontal magnetic field produced by current carrying wire, B₂ = 18 µT
To find:
New time period of oscillation, T₂
Solution:
Angular frequency of oscillation in earth's magnetic field, ω₁ = 2π/T₁
Magnetic moment of the small bar magnet, m = BAN
where B is the magnetic field, A is the area of cross-section of the magnet and N is the number of turns.
When the magnet is displaced by an angle θ from its equilibrium position, the restoring torque on the magnet is given by τ = mBsinθ
The equation of motion of the magnet is given by I(d²θ/dt²) + τ = 0
where I is the moment of inertia of the magnet.
On substituting the values, we get:
I(d²θ/dt²) + mBsinθ = 0
d²θ/dt² + (mB/I)sinθ = 0
This is a non-linear differential equation and its solution can be obtained by assuming the small angle approximation, sinθ ≈ θ.
On substituting this approximation, we get:
d²θ/dt² + (mB/I)θ = 0
This is a simple harmonic differential equation and its solution is given by:
θ = θ₀cos(ωt)
where θ₀ is the amplitude of oscillation and ω = √(mB/I) is the angular frequency of oscillation.
The time period of oscillation is given by:
T = 2π/ω
For the magnetic field produced by the current carrying wire, the new angular frequency of oscillation is given by:
ω₂ = √(m(B₁ - B₂)/I)
The new time period of oscillation is given by:
T₂ = 2π/ω₂
On substituting the values, we get:
T₂ = 4 s
Therefore, the new time period of oscillation is 4 s.

|
Explore Courses for Class 12 exam
|

|
A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer?
Question Description
A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer?.
A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer?.
Solutions for A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A vibration magnetometer placed in magneticmeridian has a small bar magnet. The magnetexecutes oscillations with a time period of 2 secin earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18microtesla is produced opposite to the earth'sfield by placing a current carrying wire, the newtime period of magnet will be [2010]a)1 sb)2 sc)3 sd)4 sCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















