Class 12 Exam > Class 12 Questions > If one penetrates a uniformly charged spheric...
Start Learning for Free
If one penetrates a uniformly charged spherical cloud electric field strength
- a)decreases directly as the distance from the centre
- b)increases directly as the distance from the centre
- c)remains constant
- d)none of the above
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
If one penetrates a uniformly charged spherical cloud electric field s...
In side the sphere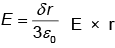 
therefore field decreases directly as the distance form the centre.
therefore field decreases directly as the distance form the centre. Most Upvoted Answer
If one penetrates a uniformly charged spherical cloud electric field s...
Electric field strength is defined as the force experienced per unit positive charge at a given point in an electric field. In the case of a uniformly charged spherical cloud, the distribution of charge is symmetrical in all directions from the center of the sphere.
The electric field strength is determined by the magnitude and distribution of charge within the cloud. As we move away from the center of the cloud, the distance between the charge and the point of observation increases. This distance plays a crucial role in determining the electric field strength.
When we penetrate the cloud and move closer to the center, the distance from the center decreases. Consequently, the electric field strength increases because the distance in the denominator of the equation for electric field strength decreases.
To understand this concept further, let's consider the equation for electric field strength (E) due to a spherical charge distribution:
E = k * (Q / r^2)
Where:
- E is the electric field strength
- k is the electrostatic constant
- Q is the total charge enclosed within a sphere of radius r
As we move towards the center of the cloud, the value of r decreases, causing the denominator (r^2) to decrease. Since the numerator (Q) remains constant for a uniformly charged cloud, the electric field strength (E) increases.
In other words, as the distance from the center decreases, the electric field strength increases. This is because the force experienced by a unit positive charge due to the surrounding charge distribution becomes stronger as we move closer to the center.
Therefore, the correct answer is option 'A' - the electric field strength decreases directly as the distance from the center.
The electric field strength is determined by the magnitude and distribution of charge within the cloud. As we move away from the center of the cloud, the distance between the charge and the point of observation increases. This distance plays a crucial role in determining the electric field strength.
When we penetrate the cloud and move closer to the center, the distance from the center decreases. Consequently, the electric field strength increases because the distance in the denominator of the equation for electric field strength decreases.
To understand this concept further, let's consider the equation for electric field strength (E) due to a spherical charge distribution:
E = k * (Q / r^2)
Where:
- E is the electric field strength
- k is the electrostatic constant
- Q is the total charge enclosed within a sphere of radius r
As we move towards the center of the cloud, the value of r decreases, causing the denominator (r^2) to decrease. Since the numerator (Q) remains constant for a uniformly charged cloud, the electric field strength (E) increases.
In other words, as the distance from the center decreases, the electric field strength increases. This is because the force experienced by a unit positive charge due to the surrounding charge distribution becomes stronger as we move closer to the center.
Therefore, the correct answer is option 'A' - the electric field strength decreases directly as the distance from the center.
|
Explore Courses for Class 12 exam
|
|
Similar Class 12 Doubts
If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer?
Question Description
If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer?.
If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer?.
Solutions for If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If one penetrates a uniformly charged spherical cloud electric field strengtha)decreases directly as the distance from the centreb)increases directly as the distance from the centrec)remains constantd)none of the aboveCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Class 12 tests.
|
|
Explore Courses for Class 12 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup