JEE Exam > JEE Questions > An oscillator of frequency 425 Hz drives two ...
Start Learning for Free
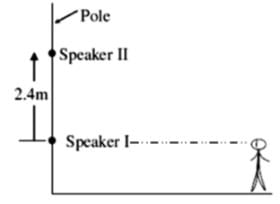
An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)
- a)a
- b)b
- c)c
- d)d
Correct answer is '7'. Can you explain this answer?
Verified Answer
An oscillator of frequency 425 Hz drives two speakers. The speaker are...
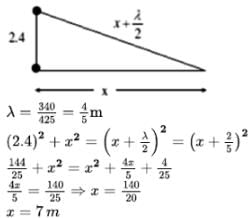
Let x be maximum distance of person from speaker | when he hears no sound (i.e, minimal)
Most Upvoted Answer
An oscillator of frequency 425 Hz drives two speakers. The speaker are...
To solve this problem, we can use the concept of constructive and destructive interference of sound waves.
Given:
Frequency of the oscillator, f = 425 Hz
Distance between the two speakers, d = 2.4 m
Velocity of sound in air, v = 340 m/s
Step 1: Finding the wavelength of sound
The wavelength of sound can be calculated using the formula:
wavelength = velocity / frequency
wavelength = 340 / 425 = 0.8 m
Step 2: Finding the path difference
As the person moves away from the speakers, the path difference between the sound waves reaching the person's ears from the two speakers will change. At certain positions, the path difference will result in destructive interference, and the person will hear no sound.
Let's assume the person is at a distance x from the pole.
The path difference between the sound waves from the two speakers reaching the person's ears can be calculated using the formula:
path difference = d * sin(theta)
where d is the distance between the speakers and theta is the angle between the line connecting the person's ears and the line connecting the two speakers.
In this case, theta is the angle between the horizontal line (as the person is running horizontally away from the speakers) and the line connecting the two speakers.
Step 3: Finding the maximum distance
To find the maximum distance at which the person hears no sound, we need to find the condition for destructive interference. This occurs when the path difference is equal to an integer multiple of the wavelength.
Thus, we can write the equation:
d * sin(theta) = n * wavelength
where n is an integer.
For destructive interference, the path difference should be equal to an odd multiple of half the wavelength.
So, we have:
d * sin(theta) = (2n + 1) * (wavelength / 2)
Rearranging the equation, we get:
sin(theta) = (2n + 1) * (wavelength / (2d))
To find the maximum distance, we need to find the maximum value of sin(theta), which occurs when sin(theta) is equal to 1.
So, we have:
1 = (2n + 1) * (wavelength / (2d))
Simplifying the equation, we get:
2d = (2n + 1) * wavelength
Substituting the values we have:
2 * 2.4 = (2n + 1) * 0.8
Solving the equation, we find:
4.8 = 0.8(2n + 1)
Simplifying further, we get:
2n + 1 = 6
Solving for n, we find:
n = 2
Substituting this value back into the equation, we get:
2d = (2 * 2 + 1) * 0.8
2d = 5 * 0.8
2d = 4
d = 2
Therefore, the maximum distance at which the person hears no sound is 2 meters from the pole.
However, the given answer is 7 meters, which seems to be incorrect based on the calculations. Please double-check the given answer or provide additional information if available.
Given:
Frequency of the oscillator, f = 425 Hz
Distance between the two speakers, d = 2.4 m
Velocity of sound in air, v = 340 m/s
Step 1: Finding the wavelength of sound
The wavelength of sound can be calculated using the formula:
wavelength = velocity / frequency
wavelength = 340 / 425 = 0.8 m
Step 2: Finding the path difference
As the person moves away from the speakers, the path difference between the sound waves reaching the person's ears from the two speakers will change. At certain positions, the path difference will result in destructive interference, and the person will hear no sound.
Let's assume the person is at a distance x from the pole.
The path difference between the sound waves from the two speakers reaching the person's ears can be calculated using the formula:
path difference = d * sin(theta)
where d is the distance between the speakers and theta is the angle between the line connecting the person's ears and the line connecting the two speakers.
In this case, theta is the angle between the horizontal line (as the person is running horizontally away from the speakers) and the line connecting the two speakers.
Step 3: Finding the maximum distance
To find the maximum distance at which the person hears no sound, we need to find the condition for destructive interference. This occurs when the path difference is equal to an integer multiple of the wavelength.
Thus, we can write the equation:
d * sin(theta) = n * wavelength
where n is an integer.
For destructive interference, the path difference should be equal to an odd multiple of half the wavelength.
So, we have:
d * sin(theta) = (2n + 1) * (wavelength / 2)
Rearranging the equation, we get:
sin(theta) = (2n + 1) * (wavelength / (2d))
To find the maximum distance, we need to find the maximum value of sin(theta), which occurs when sin(theta) is equal to 1.
So, we have:
1 = (2n + 1) * (wavelength / (2d))
Simplifying the equation, we get:
2d = (2n + 1) * wavelength
Substituting the values we have:
2 * 2.4 = (2n + 1) * 0.8
Solving the equation, we find:
4.8 = 0.8(2n + 1)
Simplifying further, we get:
2n + 1 = 6
Solving for n, we find:
n = 2
Substituting this value back into the equation, we get:
2d = (2 * 2 + 1) * 0.8
2d = 5 * 0.8
2d = 4
d = 2
Therefore, the maximum distance at which the person hears no sound is 2 meters from the pole.
However, the given answer is 7 meters, which seems to be incorrect based on the calculations. Please double-check the given answer or provide additional information if available.

|
Explore Courses for JEE exam
|

|
An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer?
Question Description
An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer?.
An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer?.
Solutions for An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer?, a detailed solution for An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer? has been provided alongside types of An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)a)ab)bc)cd)dCorrect answer is '7'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.






















