Defence Exam > Defence Questions > Suppose ω is a cube root of unity with&...
Start Learning for Free
Suppose ω is a cube root of unity with ω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?
- a)60°
- b)90°
- c)120°
- d)150°
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
Suppose ω is a cube root of unity withω≠1. Suppose P an...
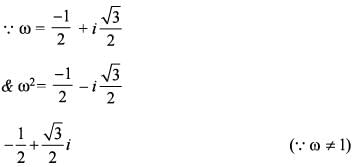
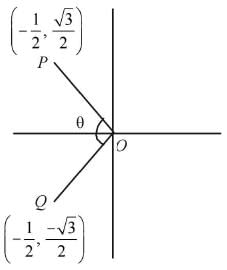
P and Q are points on complex plane. Angle between OP and OQ is
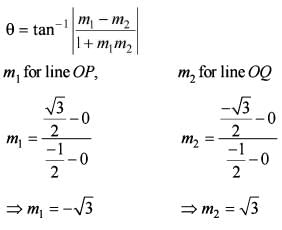
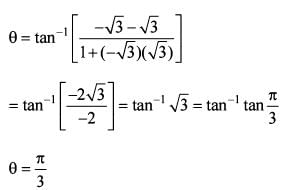
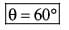
Most Upvoted Answer
Suppose ω is a cube root of unity withω≠1. Suppose P an...
Suppose we are given a set of data points {(x1, y1), (x2, y2), ..., (xn, yn)}, where xi represents the input value and yi represents the corresponding output value.
To find the equation of a line that best fits the data points, we can use linear regression. Linear regression tries to find the best-fitting line by minimizing the sum of the squared differences between the predicted values and the actual values.
The equation of a line can be written in the form y = mx + b, where m is the slope and b is the y-intercept.
The slope (m) can be calculated using the formula:
m = (nΣxy - ΣxΣy) / (nΣx^2 - (Σx)^2)
where n is the number of data points, Σxy is the sum of the products of xi and yi, Σx is the sum of all xi values, Σy is the sum of all yi values, and Σx^2 is the sum of the squares of all xi values.
The y-intercept (b) can be calculated using the formula:
b = (Σy - mΣx) / n
Once we have calculated the slope and y-intercept, we can substitute these values into the equation y = mx + b to get the equation of the line that best fits the data points.
It's important to note that linear regression assumes a linear relationship between the input and output variables. If the relationship is not linear, other regression methods such as polynomial regression or exponential regression may be more appropriate.
To find the equation of a line that best fits the data points, we can use linear regression. Linear regression tries to find the best-fitting line by minimizing the sum of the squared differences between the predicted values and the actual values.
The equation of a line can be written in the form y = mx + b, where m is the slope and b is the y-intercept.
The slope (m) can be calculated using the formula:
m = (nΣxy - ΣxΣy) / (nΣx^2 - (Σx)^2)
where n is the number of data points, Σxy is the sum of the products of xi and yi, Σx is the sum of all xi values, Σy is the sum of all yi values, and Σx^2 is the sum of the squares of all xi values.
The y-intercept (b) can be calculated using the formula:
b = (Σy - mΣx) / n
Once we have calculated the slope and y-intercept, we can substitute these values into the equation y = mx + b to get the equation of the line that best fits the data points.
It's important to note that linear regression assumes a linear relationship between the input and output variables. If the relationship is not linear, other regression methods such as polynomial regression or exponential regression may be more appropriate.
|
Explore Courses for Defence exam
|
|
Similar Defence Doubts
Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer?
Question Description
Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer? for Defence 2025 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Defence 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer?.
Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer? for Defence 2025 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Defence 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer?.
Solutions for Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer?, a detailed solution for Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Suppose ω is a cube root of unity withω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?a)60°b)90°c)120°d)150°Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice Defence tests.
|
|
Explore Courses for Defence exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup