JEE Exam > JEE Questions > A neutron moving with speed v makes a head-on...
Start Learning for Free
A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron ≈ mass of hydrogen = 1.67 x 10-27 kg
- a)22.4 eV
- b)21.4 eV
- c)20.4 eV
- d)20.1 eV
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A neutron moving with speed v makes a head-on collision with a hydroge...
Suppose the neutron and the hydrogen atom move at speeds v1 and v2 after the collision. The collision will be inelastic if a part of the kinetic energy is used to excite the atom. Suppose an energy ΔE is used in this way. Using conservation of linear momentum and energy,
mv = mv1 + mv2 ........(i)
and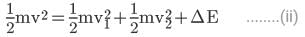
From (i),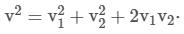
From (ii),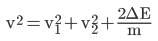
Thus,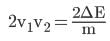
Hence, (v1 - v2)2 = (v1 + v2)2 - 4v1v2 =
As v1 - v2 must be real,
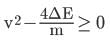
or,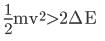
An electron in the ground state has an energy of -13.6 eV. The second energy level is -3.4 eV. Thus it would take E2 − E1 = -3.4 eV − -13.6 eV = 10.2 eV to excite the electron from the ground state to the first excited state.
The minimum energy that can be absorbed by the hydrogen atom in ground state to go in an excited state is 10.2 eV. Thus, the minimum kinetic energy of the neutron needed for an inelastic collision is
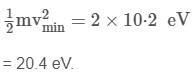
mv = mv1 + mv2 ........(i)
and
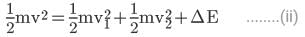
From (i),
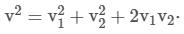
From (ii),
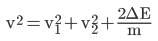
Thus,
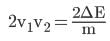
Hence, (v1 - v2)2 = (v1 + v2)2 - 4v1v2 =

As v1 - v2 must be real,
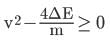
or,
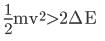
An electron in the ground state has an energy of -13.6 eV. The second energy level is -3.4 eV. Thus it would take E2 − E1 = -3.4 eV − -13.6 eV = 10.2 eV to excite the electron from the ground state to the first excited state.
The minimum energy that can be absorbed by the hydrogen atom in ground state to go in an excited state is 10.2 eV. Thus, the minimum kinetic energy of the neutron needed for an inelastic collision is
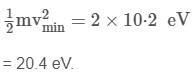
Most Upvoted Answer
A neutron moving with speed v makes a head-on collision with a hydroge...
Understanding the Problem
In this scenario, we have a neutron colliding with a hydrogen atom at rest. The goal is to determine the minimum kinetic energy required for the neutron to cause an inelastic collision.
Key Concepts
- Inelastic Collision: This type of collision allows for energy absorption, leading to a change in internal energy states or the motion of the colliding objects.
- Ground State Energy of Hydrogen Atom: The ground state of a hydrogen atom has an energy of -13.6 eV. For an inelastic collision to occur, the neutron must provide at least this energy to excite the hydrogen atom.
Energy Considerations
- The total energy before the collision consists of the kinetic energy of the neutron and the rest energy of the hydrogen atom.
- Let the kinetic energy of the neutron be K.E. = (1/2)mv^2, where m is the mass of the neutron.
Minimum Energy Requirement
- For the collision to be inelastic, the neutron must have enough kinetic energy to overcome the potential energy barrier and facilitate excitation.
- The minimum energy required for this process to occur is calculated as follows:
- The kinetic energy of the neutron must be equal to the energy required to excite the hydrogen atom from its ground state to the next available energy level.
- The energy difference to the first excited state is about 10.2 eV, but we also need to consider the binding energy when evaluating the inelastic collision.
- The effective energy threshold that enables excitation is approximately 20.4 eV, as it accounts for the ground state and the kinetic energy of the neutron.
Conclusion
Thus, the minimum kinetic energy that the neutron must possess for an inelastic collision with the hydrogen atom is approximately 20.4 eV, which corresponds to option C.
In this scenario, we have a neutron colliding with a hydrogen atom at rest. The goal is to determine the minimum kinetic energy required for the neutron to cause an inelastic collision.
Key Concepts
- Inelastic Collision: This type of collision allows for energy absorption, leading to a change in internal energy states or the motion of the colliding objects.
- Ground State Energy of Hydrogen Atom: The ground state of a hydrogen atom has an energy of -13.6 eV. For an inelastic collision to occur, the neutron must provide at least this energy to excite the hydrogen atom.
Energy Considerations
- The total energy before the collision consists of the kinetic energy of the neutron and the rest energy of the hydrogen atom.
- Let the kinetic energy of the neutron be K.E. = (1/2)mv^2, where m is the mass of the neutron.
Minimum Energy Requirement
- For the collision to be inelastic, the neutron must have enough kinetic energy to overcome the potential energy barrier and facilitate excitation.
- The minimum energy required for this process to occur is calculated as follows:
- The kinetic energy of the neutron must be equal to the energy required to excite the hydrogen atom from its ground state to the next available energy level.
- The energy difference to the first excited state is about 10.2 eV, but we also need to consider the binding energy when evaluating the inelastic collision.
- The effective energy threshold that enables excitation is approximately 20.4 eV, as it accounts for the ground state and the kinetic energy of the neutron.
Conclusion
Thus, the minimum kinetic energy that the neutron must possess for an inelastic collision with the hydrogen atom is approximately 20.4 eV, which corresponds to option C.
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.

|
Explore Courses for JEE exam
|

|
A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer?
Question Description
A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer?.
A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer?.
Solutions for A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A neutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest. Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron≈mass of hydrogen = 1.67 x 10-27kga)22.4 eVb)21.4 eVc)20.4 eVd)20.1 eVCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.






















