Defence Exam > Defence Questions > If the data are moderately non-symmetrical, t...
Start Learning for Free
If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?
- a)2 x Standard deviation = 5 x Mean deviation
- b)5 x Standard deviation = 2 x Mean deviation
- c)4 x Standard deviation = 5 x Mean deviation
- d)5 x Standard deviation = 4 x Mean deviation
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
If the data are moderately non-symmetrical, then which one of the foll...
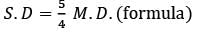
Most Upvoted Answer
If the data are moderately non-symmetrical, then which one of the foll...
Understanding the Empirical Relationships
When dealing with measures of dispersion in statistics, two common metrics are the Standard Deviation (SD) and the Mean Deviation (MD). Their relationship can provide insights into the data distribution, especially when the data is moderately non-symmetrical.
Key Concepts
- Standard Deviation (SD): Measures the average distance of each data point from the mean. It is sensitive to extreme values.
- Mean Deviation (MD): Measures the average distance of each data point from the mean, but it takes absolute values, making it less influenced by outliers.
Relationship in Moderately Non-Symmetrical Data
In moderately non-symmetrical datasets, empirical relationships can often be established. Option 'D' states:
- 5 x Standard Deviation = 4 x Mean Deviation
This relationship suggests that in such distributions, the standard deviation tends to be slightly larger than the mean deviation, reflecting the influence of asymmetry in the data.
Why is Option D Correct?
- Impact of Skewness: In moderately non-symmetrical distributions, the skewness affects the SD more than the MD. Therefore, SD being a multiple of MD makes logical sense.
- Empirical Evidence: Empirical studies on various distributions have shown that this relationship holds true, particularly in practical applications involving real-world data.
Conclusion
Understanding these relationships is crucial for properly interpreting data. In moderately non-symmetrical distributions, the established relationship of 5 x SD = 4 x MD provides a useful rule of thumb for statisticians and analysts working in the Defence category or any data-driven field.
When dealing with measures of dispersion in statistics, two common metrics are the Standard Deviation (SD) and the Mean Deviation (MD). Their relationship can provide insights into the data distribution, especially when the data is moderately non-symmetrical.
Key Concepts
- Standard Deviation (SD): Measures the average distance of each data point from the mean. It is sensitive to extreme values.
- Mean Deviation (MD): Measures the average distance of each data point from the mean, but it takes absolute values, making it less influenced by outliers.
Relationship in Moderately Non-Symmetrical Data
In moderately non-symmetrical datasets, empirical relationships can often be established. Option 'D' states:
- 5 x Standard Deviation = 4 x Mean Deviation
This relationship suggests that in such distributions, the standard deviation tends to be slightly larger than the mean deviation, reflecting the influence of asymmetry in the data.
Why is Option D Correct?
- Impact of Skewness: In moderately non-symmetrical distributions, the skewness affects the SD more than the MD. Therefore, SD being a multiple of MD makes logical sense.
- Empirical Evidence: Empirical studies on various distributions have shown that this relationship holds true, particularly in practical applications involving real-world data.
Conclusion
Understanding these relationships is crucial for properly interpreting data. In moderately non-symmetrical distributions, the established relationship of 5 x SD = 4 x MD provides a useful rule of thumb for statisticians and analysts working in the Defence category or any data-driven field.

|
Explore Courses for Defence exam
|

|
Similar Defence Doubts
If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer?
Question Description
If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer?.
If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer?.
Solutions for If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If the data are moderately non-symmetrical, then which one of the following empirical relationships is correct?a)2 x Standard deviation = 5 x Mean deviationb)5 x Standard deviation = 2 x Mean deviationc)4 x Standard deviation = 5 x Mean deviationd)5 x Standard deviation = 4 x Mean deviationCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Defence tests.

|
Explore Courses for Defence exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















