Mechanical Engineering Exam > Mechanical Engineering Questions > The shear stress-strain graph for a Newtonian...
Start Learning for Free
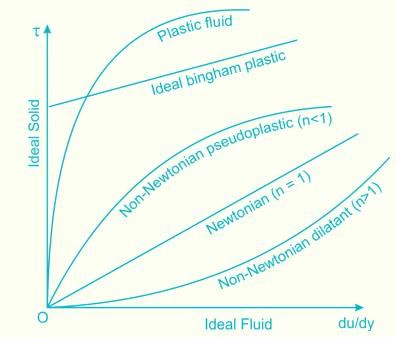
The shear stress-strain graph for a Newtonian fluid is a
- a)Straight line
- b)Parabolic Curve
- c)Hyperbolic Curve
- d)Elliptical
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The shear stress-strain graph for a Newtonian fluid is aa)Straight lin...
Newtonian fluids defined as fluids for which the shear stress is linearly proportional to the shear strain rate. Newtonian fluids are analogous to elastic solids (Hooke’s law: stress proportional to strain). Any common fluids, such as air and other gases, water, kerosene, gasoline, and other oil-based liquids, are Newtonian fluids.
Fluids for which the shear stress is not linearly related to the shear strain rate are called non- Newtonian fluids. examples include slurries and colloidal suspensions, polymer solutions, blood, paste, and cake batter.
Most Upvoted Answer
The shear stress-strain graph for a Newtonian fluid is aa)Straight lin...
The shear stress-strain graph for a Newtonian fluid is a straight line. This can be explained by considering the properties of Newtonian fluids and their behavior under shear stress.
1. Newtonian Fluids:
- Newtonian fluids are characterized by their constant viscosity, meaning that the shear stress is directly proportional to the shear rate.
- Shear stress (τ) is defined as the force per unit area that acts parallel to the surface of an object when it is subjected to shear deformation.
- Shear rate (γ) is defined as the rate of change of deformation with respect to time.
2. Relationship between Shear Stress and Shear Rate:
- In Newtonian fluids, the relationship between shear stress and shear rate is linear, represented by the equation τ = μγ, where μ is the dynamic viscosity of the fluid.
- The dynamic viscosity is a measure of a fluid's resistance to shear or flow.
3. Shear Stress-Strain Graph:
- When a Newtonian fluid is subjected to shear stress, it deforms continuously and the shear rate increases linearly with increasing shear stress.
- As a result, the shear stress-strain graph for a Newtonian fluid is a straight line passing through the origin.
- The slope of the line represents the dynamic viscosity of the fluid.
4. Example:
- Let's consider an example of a Newtonian fluid flowing between two parallel plates.
- Initially, when no shear stress is applied, the fluid does not deform and the shear rate is zero.
- As the shear stress is gradually increased, the fluid starts to deform, and the shear rate increases linearly.
- The slope of the resulting shear stress-strain graph represents the dynamic viscosity of the fluid.
- If the fluid has a higher dynamic viscosity, the slope of the graph will be steeper, indicating a higher resistance to shear deformation.
In conclusion, the shear stress-strain graph for a Newtonian fluid is a straight line because of the linear relationship between shear stress and shear rate in these fluids. This behavior is characteristic of fluids with constant viscosity, where the slope of the graph represents the dynamic viscosity of the fluid.
1. Newtonian Fluids:
- Newtonian fluids are characterized by their constant viscosity, meaning that the shear stress is directly proportional to the shear rate.
- Shear stress (τ) is defined as the force per unit area that acts parallel to the surface of an object when it is subjected to shear deformation.
- Shear rate (γ) is defined as the rate of change of deformation with respect to time.
2. Relationship between Shear Stress and Shear Rate:
- In Newtonian fluids, the relationship between shear stress and shear rate is linear, represented by the equation τ = μγ, where μ is the dynamic viscosity of the fluid.
- The dynamic viscosity is a measure of a fluid's resistance to shear or flow.
3. Shear Stress-Strain Graph:
- When a Newtonian fluid is subjected to shear stress, it deforms continuously and the shear rate increases linearly with increasing shear stress.
- As a result, the shear stress-strain graph for a Newtonian fluid is a straight line passing through the origin.
- The slope of the line represents the dynamic viscosity of the fluid.
4. Example:
- Let's consider an example of a Newtonian fluid flowing between two parallel plates.
- Initially, when no shear stress is applied, the fluid does not deform and the shear rate is zero.
- As the shear stress is gradually increased, the fluid starts to deform, and the shear rate increases linearly.
- The slope of the resulting shear stress-strain graph represents the dynamic viscosity of the fluid.
- If the fluid has a higher dynamic viscosity, the slope of the graph will be steeper, indicating a higher resistance to shear deformation.
In conclusion, the shear stress-strain graph for a Newtonian fluid is a straight line because of the linear relationship between shear stress and shear rate in these fluids. This behavior is characteristic of fluids with constant viscosity, where the slope of the graph represents the dynamic viscosity of the fluid.
Attention Mechanical Engineering Students!
To make sure you are not studying endlessly, EduRev has designed Mechanical Engineering study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Mechanical Engineering.
|
Explore Courses for Mechanical Engineering exam
|
|
Similar Mechanical Engineering Doubts
Top Courses for Mechanical EngineeringView all
The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer?
Question Description
The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer?.
The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer?.
Solutions for The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The shear stress-strain graph for a Newtonian fluid is aa)Straight lineb)Parabolic Curvec)Hyperbolic Curved)EllipticalCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.
|
|
Explore Courses for Mechanical Engineering exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup