IIT JAM Exam > IIT JAM Questions > A kingfisher is flying 36 m high from the wat...
Start Learning for Free
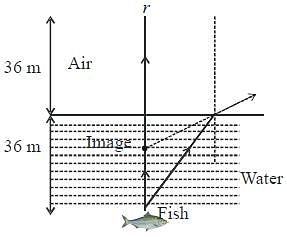
A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}
- a)27 m
- b)48 m
- c)36 m
- d)12 m
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A kingfisher is flying 36 m high from the water surface of a pond. A f...
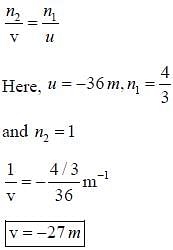
Most Upvoted Answer
A kingfisher is flying 36 m high from the water surface of a pond. A f...
To solve this problem, we can use the concept of refraction. Refraction is the bending of light as it passes from one medium to another with a different refractive index. In this case, the light travels from air (where the kingfisher is) to water (where the fish is).
Let's break down the problem into steps:
Step 1: Determine the path of light
The light from the fish travels from water to air and then reaches the kingfisher's eyes. We need to find the depth at which the fish seems to be to the kingfisher.
Step 2: Apply the Snell's law
Snell's law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is equal to the ratio of the speeds of light in the two media. In this case, we can assume that the angle of incidence and the angle of refraction are small, so we can use the simplified form of Snell's law:
n1 * sinθ1 = n2 * sinθ2
where n1 and n2 are the refractive indices of the two media, and θ1 and θ2 are the angles of incidence and refraction, respectively.
Step 3: Apply Snell's law to find the depth
In this problem, the light travels from water (n1 = 4/3) to air (n2 = 1). We know that the angle of incidence is 90 degrees (as the light is coming vertically upwards) and we need to find the angle of refraction.
Using Snell's law, we can write:
(4/3) * sin(90 degrees) = 1 * sinθ2
Simplifying the equation, we find:
(4/3) * 1 = sinθ2
θ2 = sin^(-1)(4/3) ≈ 53.13 degrees
Step 4: Calculate the depth of the fish
Now, we can use trigonometry to find the depth at which the fish seems to be to the kingfisher.
Using the tangent function, we have:
tan(θ2) = depth of fish / height of kingfisher
tan(53.13 degrees) = depth of fish / 36 m
depth of fish = tan(53.13 degrees) * 36 m ≈ 26.99 m
Rounding this value to the nearest meter gives us 27 m, which is the correct answer.
Therefore, the fish seems to be at a depth of 27 m from the water surface to the kingfisher.
Let's break down the problem into steps:
Step 1: Determine the path of light
The light from the fish travels from water to air and then reaches the kingfisher's eyes. We need to find the depth at which the fish seems to be to the kingfisher.
Step 2: Apply the Snell's law
Snell's law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is equal to the ratio of the speeds of light in the two media. In this case, we can assume that the angle of incidence and the angle of refraction are small, so we can use the simplified form of Snell's law:
n1 * sinθ1 = n2 * sinθ2
where n1 and n2 are the refractive indices of the two media, and θ1 and θ2 are the angles of incidence and refraction, respectively.
Step 3: Apply Snell's law to find the depth
In this problem, the light travels from water (n1 = 4/3) to air (n2 = 1). We know that the angle of incidence is 90 degrees (as the light is coming vertically upwards) and we need to find the angle of refraction.
Using Snell's law, we can write:
(4/3) * sin(90 degrees) = 1 * sinθ2
Simplifying the equation, we find:
(4/3) * 1 = sinθ2
θ2 = sin^(-1)(4/3) ≈ 53.13 degrees
Step 4: Calculate the depth of the fish
Now, we can use trigonometry to find the depth at which the fish seems to be to the kingfisher.
Using the tangent function, we have:
tan(θ2) = depth of fish / height of kingfisher
tan(53.13 degrees) = depth of fish / 36 m
depth of fish = tan(53.13 degrees) * 36 m ≈ 26.99 m
Rounding this value to the nearest meter gives us 27 m, which is the correct answer.
Therefore, the fish seems to be at a depth of 27 m from the water surface to the kingfisher.

|
Explore Courses for IIT JAM exam
|

|
A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer?
Question Description
A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer? for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer?.
A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer? for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer?.
Solutions for A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for IIT JAM.
Download more important topics, notes, lectures and mock test series for IIT JAM Exam by signing up for free.
Here you can find the meaning of A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A kingfisher is flying 36 m high from the water surface of a pond. A fish is 36 m deep in water from the water surface. At what depth from the water surface, the fish seems to be to the kingfisher {refractive index of water is 4/3}a)27 mb)48 mc)36 md)12 mCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice IIT JAM tests.

|
Explore Courses for IIT JAM exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
















