IIT JAM Exam > IIT JAM Questions > A convex lens of focal length 30 cm and a con...
Start Learning for Free
A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]
Correct answer is '20'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A convex lens of focal length 30 cm and a concave lens of focal length...
Parallel rays coming on the convex lens will converge on the focus, i.e.. 30 cm right to the convexlens. If these rays seem to be approaching the focus of concave lens, they will emerge as parallel rays.
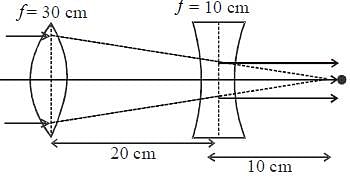
So. the distance between lenses
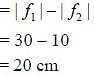

So. the distance between lenses
Most Upvoted Answer
A convex lens of focal length 30 cm and a concave lens of focal length...
Given data:
- Focal length of convex lens, f1 = 30 cm
- Focal length of concave lens, f2 = -10 cm (negative sign indicates concave lens)
- Distance between the lenses, d = ?
Concept:
When a parallel beam of light passes through a convex lens, it converges at a point called the focal point. Similarly, when a parallel beam of light passes through a concave lens, the light rays diverge as if they are coming from a point called the focal point.
When the convex lens and concave lens are placed at a certain distance from each other, the converging effect of the convex lens can be balanced by the diverging effect of the concave lens. This results in the light rays leaving the concave lens parallel to the principal axis.
Calculating the distance between the lenses (d):
To find the value of d, we need to consider the lens formula and the lens-maker's formula.
Lens formula:
The lens formula relates the object distance (u), image distance (v), and the focal length (f) of a lens. It is given by:
1/v - 1/u = 1/f
For the convex lens, the object distance (u1) is infinity because the light rays are parallel. Therefore, the equation becomes:
1/v1 - 1/infinity = 1/f1
1/v1 = 1/f1
v1 = f1
Lens-maker's formula:
The lens-maker's formula relates the focal length (f), refractive index of the lens material (μ), and the radii of curvature of the lens surfaces (R1 and R2). It is given by:
1/f = (μ - 1) * (1/R1 - 1/R2)
For the concave lens, the focal length (f2) is given as -10 cm. Since the concave lens is a diverging lens, the focal length is negative. Therefore, the equation becomes:
1/-10 = (μ - 1) * (1/R1 - 1/R2)
1/-10 = (μ - 1) * (1/R1 + 1/R2)
Assuming the radii of curvature are equal for simplicity (R1 = R2 = R), we can rewrite the equation as:
1/-10 = (μ - 1) * (2/R)
Simplifying further:
-1/10 = (μ - 1) * (2/R)
-1/10 = (μ - 1) * (2/2R)
-1/10 = (μ - 1) * (1/R)
Balancing the converging and diverging effects:
To balance the converging effect of the convex lens with the diverging effect of the concave lens, the image formed by the convex lens should act as the object for the concave lens. Therefore, the image distance (v1) calculated earlier becomes the object distance (u2) for the concave lens.
Applying the lens formula for the concave lens:
1/v2 - 1/u2 = 1/f2
1/v2 - 1/v1 = 1/f2
1/v2 - 1/f1 = 1/f2
- Focal length of convex lens, f1 = 30 cm
- Focal length of concave lens, f2 = -10 cm (negative sign indicates concave lens)
- Distance between the lenses, d = ?
Concept:
When a parallel beam of light passes through a convex lens, it converges at a point called the focal point. Similarly, when a parallel beam of light passes through a concave lens, the light rays diverge as if they are coming from a point called the focal point.
When the convex lens and concave lens are placed at a certain distance from each other, the converging effect of the convex lens can be balanced by the diverging effect of the concave lens. This results in the light rays leaving the concave lens parallel to the principal axis.
Calculating the distance between the lenses (d):
To find the value of d, we need to consider the lens formula and the lens-maker's formula.
Lens formula:
The lens formula relates the object distance (u), image distance (v), and the focal length (f) of a lens. It is given by:
1/v - 1/u = 1/f
For the convex lens, the object distance (u1) is infinity because the light rays are parallel. Therefore, the equation becomes:
1/v1 - 1/infinity = 1/f1
1/v1 = 1/f1
v1 = f1
Lens-maker's formula:
The lens-maker's formula relates the focal length (f), refractive index of the lens material (μ), and the radii of curvature of the lens surfaces (R1 and R2). It is given by:
1/f = (μ - 1) * (1/R1 - 1/R2)
For the concave lens, the focal length (f2) is given as -10 cm. Since the concave lens is a diverging lens, the focal length is negative. Therefore, the equation becomes:
1/-10 = (μ - 1) * (1/R1 - 1/R2)
1/-10 = (μ - 1) * (1/R1 + 1/R2)
Assuming the radii of curvature are equal for simplicity (R1 = R2 = R), we can rewrite the equation as:
1/-10 = (μ - 1) * (2/R)
Simplifying further:
-1/10 = (μ - 1) * (2/R)
-1/10 = (μ - 1) * (2/2R)
-1/10 = (μ - 1) * (1/R)
Balancing the converging and diverging effects:
To balance the converging effect of the convex lens with the diverging effect of the concave lens, the image formed by the convex lens should act as the object for the concave lens. Therefore, the image distance (v1) calculated earlier becomes the object distance (u2) for the concave lens.
Applying the lens formula for the concave lens:
1/v2 - 1/u2 = 1/f2
1/v2 - 1/v1 = 1/f2
1/v2 - 1/f1 = 1/f2

|
Explore Courses for IIT JAM exam
|

|
A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer?
Question Description
A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer? for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer? covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer?.
A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer? for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer? covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer?.
Solutions for A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer? in English & in Hindi are available as part of our courses for IIT JAM.
Download more important topics, notes, lectures and mock test series for IIT JAM Exam by signing up for free.
Here you can find the meaning of A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer?, a detailed solution for A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer? has been provided alongside types of A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A convex lens of focal length 30 cm and a concave lens of focal length 10 cm are kept at a distance d apart in the air. If light rays parallel to the principal axis are falling on the convex lens, the value of d for which light rays going out from the concave lens are also parallel to the principal axis is ______ (give your answer in cms) [the answer is an integer]Correct answer is '20'. Can you explain this answer? tests, examples and also practice IIT JAM tests.

|
Explore Courses for IIT JAM exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
















