Class 9 Exam > Class 9 Questions > show that the figure formed by joining the mi...
Start Learning for Free
show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle
? Related: Hots Questions- Quadrilaterals
Verified Answer
show that the figure formed by joining the mid point of the sides of r...
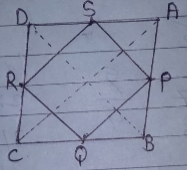
Let ABCD be a rhombus and P,Q,R and S be the mid-points of sides AB,BC,CD and DA respectively.
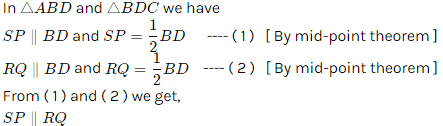

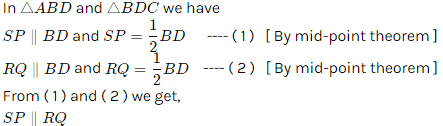


 This question is part of UPSC exam. View all Class 9 courses
This question is part of UPSC exam. View all Class 9 courses
Most Upvoted Answer
show that the figure formed by joining the mid point of the sides of r...
Introduction:
A rhombus is a quadrilateral with all sides of equal length. The midpoints of the sides of a rhombus can be joined to form a figure. We need to prove that this figure is a rectangle.
Proof:
Let ABCD be a rhombus, and let E, F, G, and H be the midpoints of the sides AB, BC, CD, and DA respectively.
Step 1: Show that all sides are parallel
To prove that the figure formed by joining the midpoints is a rectangle, we need to show that the opposite sides are parallel.
- Draw diagonal AC, which bisects each other at point O.
- Since ABCD is a rhombus, all sides are equal in length.
- By the midpoint theorem, EO is parallel to AD, and FO is parallel to AB.
- Also, GO is parallel to BC, and HO is parallel to CD.
- Therefore, opposite sides EO and GO are parallel, and FO and HO are parallel.
Step 2: Show that all angles are right angles
To prove that the figure is a rectangle, we need to show that all angles are right angles.
- Since diagonal AC bisects each other at point O, it divides the figure into four triangles: AEO, BFO, CGO, and DHO.
- Since ABCD is a rhombus, all angles are equal to 90 degrees.
- Therefore, angles at E, F, G, and H are all right angles.
Step 3: Conclusion
- We have shown that the opposite sides are parallel and all angles are right angles.
- A quadrilateral with opposite sides parallel and all angles right angles is a rectangle.
- Therefore, the figure formed by joining the midpoints of the sides of a rhombus successively is a rectangle.
Summary:
By proving that the opposite sides are parallel and all angles are right angles, we have shown that the figure formed by joining the midpoints of the sides of a rhombus successively is a rectangle.
A rhombus is a quadrilateral with all sides of equal length. The midpoints of the sides of a rhombus can be joined to form a figure. We need to prove that this figure is a rectangle.
Proof:
Let ABCD be a rhombus, and let E, F, G, and H be the midpoints of the sides AB, BC, CD, and DA respectively.
Step 1: Show that all sides are parallel
To prove that the figure formed by joining the midpoints is a rectangle, we need to show that the opposite sides are parallel.
- Draw diagonal AC, which bisects each other at point O.
- Since ABCD is a rhombus, all sides are equal in length.
- By the midpoint theorem, EO is parallel to AD, and FO is parallel to AB.
- Also, GO is parallel to BC, and HO is parallel to CD.
- Therefore, opposite sides EO and GO are parallel, and FO and HO are parallel.
Step 2: Show that all angles are right angles
To prove that the figure is a rectangle, we need to show that all angles are right angles.
- Since diagonal AC bisects each other at point O, it divides the figure into four triangles: AEO, BFO, CGO, and DHO.
- Since ABCD is a rhombus, all angles are equal to 90 degrees.
- Therefore, angles at E, F, G, and H are all right angles.
Step 3: Conclusion
- We have shown that the opposite sides are parallel and all angles are right angles.
- A quadrilateral with opposite sides parallel and all angles right angles is a rectangle.
- Therefore, the figure formed by joining the midpoints of the sides of a rhombus successively is a rectangle.
Summary:
By proving that the opposite sides are parallel and all angles are right angles, we have shown that the figure formed by joining the midpoints of the sides of a rhombus successively is a rectangle.
Attention Class 9 Students!
To make sure you are not studying endlessly, EduRev has designed Class 9 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 9.

|
Explore Courses for Class 9 exam
|

|
show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals?
Question Description
show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals?.
show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals?.
Solutions for show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals? defined & explained in the simplest way possible. Besides giving the explanation of
show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals?, a detailed solution for show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals? has been provided alongside types of show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals? theory, EduRev gives you an
ample number of questions to practice show that the figure formed by joining the mid point of the sides of rhombus successively is a rectangle Related: Hots Questions- Quadrilaterals? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























