JEE Exam > JEE Questions > A monoatomic ideal gas undergoes a process in...
Start Learning for Free
A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas
Verified Answer
A monoatomic ideal gas undergoes a process in which the ratio of P to ...
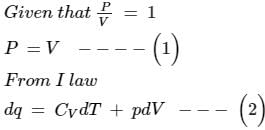

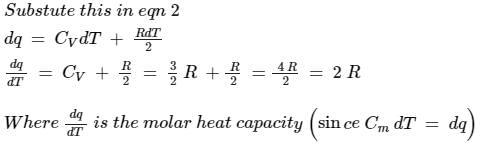
 This question is part of UPSC exam. View all JEE courses
This question is part of UPSC exam. View all JEE courses
Most Upvoted Answer
A monoatomic ideal gas undergoes a process in which the ratio of P to ...
Introduction:
The molar heat capacity of a substance is the amount of heat energy required to raise the temperature of one mole of the substance by one degree Celsius (or one Kelvin). It is an important property that helps us understand how heat energy is transferred and stored within a substance.
Explanation:
In this given scenario, we have a monoatomic ideal gas undergoing a process where the ratio of pressure (P) to volume (V) is constant and equal to 1. Let's analyze the molar heat capacity of this gas.
1. Definition of molar heat capacity:
The molar heat capacity (C) can be defined as the ratio of the amount of heat energy (Q) transferred to a substance to the change in temperature (ΔT) of the substance. Mathematically, C = Q/ΔT.
2. Constant P/V ratio:
In this process, the ratio of pressure to volume (P/V) is constant and equal to 1. This implies that as the volume increases, the pressure also increases proportionally to maintain the constant ratio.
3. Heat transfer in an ideal gas:
For an ideal gas, the heat transfer occurs through changes in internal energy (U) and work done (W). The change in internal energy is given by the equation ΔU = Q - W, where Q is the heat energy transferred to the gas and W is the work done by or on the gas.
4. No work done:
Since the P/V ratio is constant and equal to 1, there is no work done by or on the gas during this process. This means that the entire heat energy transferred to the gas is utilized to change its internal energy.
5. Relationship with molar heat capacity:
In this scenario, since all the heat energy is used to change the internal energy (ΔU) of the gas, we can say that ΔU = Q. Therefore, the molar heat capacity (C) can be expressed as C = ΔU/ΔT.
6. Calculation of molar heat capacity:
To calculate the molar heat capacity, we need to consider the change in internal energy ΔU of the gas. Since the gas is monoatomic, the change in internal energy can be expressed as ΔU = (3/2) nR ΔT, where n is the number of moles and R is the ideal gas constant.
7. Final expression for molar heat capacity:
Substituting the expression for ΔU into the equation for molar heat capacity, we get C = (3/2) nR ΔT / ΔT = (3/2) nR.
Conclusion:
In conclusion, for a monoatomic ideal gas undergoing a process where the ratio of P to V is constant and equal to 1, the molar heat capacity is given by C = (3/2) nR, where n is the number of moles and R is the ideal gas constant. This molar heat capacity represents the amount of heat energy required to raise the temperature of one mole of the gas by one degree Celsius (or one Kelvin).
The molar heat capacity of a substance is the amount of heat energy required to raise the temperature of one mole of the substance by one degree Celsius (or one Kelvin). It is an important property that helps us understand how heat energy is transferred and stored within a substance.
Explanation:
In this given scenario, we have a monoatomic ideal gas undergoing a process where the ratio of pressure (P) to volume (V) is constant and equal to 1. Let's analyze the molar heat capacity of this gas.
1. Definition of molar heat capacity:
The molar heat capacity (C) can be defined as the ratio of the amount of heat energy (Q) transferred to a substance to the change in temperature (ΔT) of the substance. Mathematically, C = Q/ΔT.
2. Constant P/V ratio:
In this process, the ratio of pressure to volume (P/V) is constant and equal to 1. This implies that as the volume increases, the pressure also increases proportionally to maintain the constant ratio.
3. Heat transfer in an ideal gas:
For an ideal gas, the heat transfer occurs through changes in internal energy (U) and work done (W). The change in internal energy is given by the equation ΔU = Q - W, where Q is the heat energy transferred to the gas and W is the work done by or on the gas.
4. No work done:
Since the P/V ratio is constant and equal to 1, there is no work done by or on the gas during this process. This means that the entire heat energy transferred to the gas is utilized to change its internal energy.
5. Relationship with molar heat capacity:
In this scenario, since all the heat energy is used to change the internal energy (ΔU) of the gas, we can say that ΔU = Q. Therefore, the molar heat capacity (C) can be expressed as C = ΔU/ΔT.
6. Calculation of molar heat capacity:
To calculate the molar heat capacity, we need to consider the change in internal energy ΔU of the gas. Since the gas is monoatomic, the change in internal energy can be expressed as ΔU = (3/2) nR ΔT, where n is the number of moles and R is the ideal gas constant.
7. Final expression for molar heat capacity:
Substituting the expression for ΔU into the equation for molar heat capacity, we get C = (3/2) nR ΔT / ΔT = (3/2) nR.
Conclusion:
In conclusion, for a monoatomic ideal gas undergoing a process where the ratio of P to V is constant and equal to 1, the molar heat capacity is given by C = (3/2) nR, where n is the number of moles and R is the ideal gas constant. This molar heat capacity represents the amount of heat energy required to raise the temperature of one mole of the gas by one degree Celsius (or one Kelvin).

|
Explore Courses for JEE exam
|

|
Similar JEE Doubts
A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas
Question Description
A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas.
A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas.
Solutions for A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas defined & explained in the simplest way possible. Besides giving the explanation of
A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas, a detailed solution for A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas has been provided alongside types of A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas theory, EduRev gives you an
ample number of questions to practice A monoatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1. What is the molar heat capacity of the gas tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























