Class 12 Exam > Class 12 Questions > What is the Maxwell modifications of ampere l...
Start Learning for Free
What is the Maxwell modifications of ampere law
Verified Answer
What is the Maxwell modifications of ampere law


 This question is part of UPSC exam. View all Class 12 courses
This question is part of UPSC exam. View all Class 12 courses
Most Upvoted Answer
What is the Maxwell modifications of ampere law
Maxwell's Modifications of Ampere's Law
Maxwell's modifications of Ampere's Law are a set of additional terms introduced by James Clerk Maxwell to account for the existence of displacement currents and to reconcile Ampere's Law with the laws of electromagnetic induction. These modifications play a crucial role in understanding the behavior of electromagnetic fields and the propagation of electromagnetic waves.
1. Ampere's Law
Ampere's Law states that the line integral of the magnetic field around a closed loop is equal to the net current passing through the loop. Mathematically, it is expressed as:
∮ B · dl = μ₀I,
where B is the magnetic field, dl is an infinitesimal element of the closed loop, μ₀ is the permeability of free space, and I is the net current enclosed by the loop.
2. Displacement Current
Maxwell introduced the concept of displacement current to account for the changing electric fields in a region. According to Maxwell, a changing electric field induces a magnetic field, just as a changing magnetic field induces an electric field. This displacement current is expressed as:
Id = ε₀(dE/dt),
where Id is the displacement current, ε₀ is the permittivity of free space, and dE/dt represents the rate of change of the electric field with respect to time.
3. Maxwell's Modification
To incorporate the displacement current into Ampere's Law, Maxwell modified it by adding the displacement current term. The modified form of Ampere's Law, known as Maxwell's Ampere's Law, is given by:
∮ B · dl = μ₀(I + Id),
where Id represents the displacement current. This modification allows Ampere's Law to account for both conduction currents (I) and displacement currents (Id) present in a given region.
4. Electromagnetic Waves
One of the significant consequences of Maxwell's modifications is the prediction and explanation of electromagnetic waves. Maxwell's equations, including the modified Ampere's Law, indicate that changing electric fields give rise to magnetic fields, and vice versa. This interplay between electric and magnetic fields leads to the self-propagation of electromagnetic waves through space, with the speed of light being a fundamental constant of nature.
Conclusion
Maxwell's modifications of Ampere's Law, incorporating the concept of displacement current, provide a more comprehensive understanding of the behavior of electromagnetic fields. These modifications not only reconcile Ampere's Law with the laws of electromagnetic induction but also allow for the prediction and explanation of electromagnetic waves. By considering both conduction currents and displacement currents, Maxwell's Ampere's Law forms an integral part of Maxwell's equations, which describe the fundamental principles governing electromagnetism.
Maxwell's modifications of Ampere's Law are a set of additional terms introduced by James Clerk Maxwell to account for the existence of displacement currents and to reconcile Ampere's Law with the laws of electromagnetic induction. These modifications play a crucial role in understanding the behavior of electromagnetic fields and the propagation of electromagnetic waves.
1. Ampere's Law
Ampere's Law states that the line integral of the magnetic field around a closed loop is equal to the net current passing through the loop. Mathematically, it is expressed as:
∮ B · dl = μ₀I,
where B is the magnetic field, dl is an infinitesimal element of the closed loop, μ₀ is the permeability of free space, and I is the net current enclosed by the loop.
2. Displacement Current
Maxwell introduced the concept of displacement current to account for the changing electric fields in a region. According to Maxwell, a changing electric field induces a magnetic field, just as a changing magnetic field induces an electric field. This displacement current is expressed as:
Id = ε₀(dE/dt),
where Id is the displacement current, ε₀ is the permittivity of free space, and dE/dt represents the rate of change of the electric field with respect to time.
3. Maxwell's Modification
To incorporate the displacement current into Ampere's Law, Maxwell modified it by adding the displacement current term. The modified form of Ampere's Law, known as Maxwell's Ampere's Law, is given by:
∮ B · dl = μ₀(I + Id),
where Id represents the displacement current. This modification allows Ampere's Law to account for both conduction currents (I) and displacement currents (Id) present in a given region.
4. Electromagnetic Waves
One of the significant consequences of Maxwell's modifications is the prediction and explanation of electromagnetic waves. Maxwell's equations, including the modified Ampere's Law, indicate that changing electric fields give rise to magnetic fields, and vice versa. This interplay between electric and magnetic fields leads to the self-propagation of electromagnetic waves through space, with the speed of light being a fundamental constant of nature.
Conclusion
Maxwell's modifications of Ampere's Law, incorporating the concept of displacement current, provide a more comprehensive understanding of the behavior of electromagnetic fields. These modifications not only reconcile Ampere's Law with the laws of electromagnetic induction but also allow for the prediction and explanation of electromagnetic waves. By considering both conduction currents and displacement currents, Maxwell's Ampere's Law forms an integral part of Maxwell's equations, which describe the fundamental principles governing electromagnetism.
Community Answer
What is the Maxwell modifications of ampere law
Maxwell modified it in order to include the effect of time-varying electric fields. Time-varying electric flux creates a magnetic field, just as does conduction current. One can take this effect into account by adding an extra term, , to the RHS of Ampere's Law (making it the ``Ampere-Maxwell'' Law. Here I d is the ``displacement current'',
, to the RHS of Ampere's Law (making it the ``Ampere-Maxwell'' Law. Here I d is the ``displacement current'', 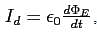 , a kind of equivalent current associated with a changing electric flux.
, a kind of equivalent current associated with a changing electric flux.
 , to the RHS of Ampere's Law (making it the ``Ampere-Maxwell'' Law. Here I d is the ``displacement current'',
, to the RHS of Ampere's Law (making it the ``Ampere-Maxwell'' Law. Here I d is the ``displacement current'', 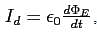 , a kind of equivalent current associated with a changing electric flux.
, a kind of equivalent current associated with a changing electric flux.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
What is the Maxwell modifications of ampere law
Question Description
What is the Maxwell modifications of ampere law for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about What is the Maxwell modifications of ampere law covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the Maxwell modifications of ampere law.
What is the Maxwell modifications of ampere law for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about What is the Maxwell modifications of ampere law covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the Maxwell modifications of ampere law.
Solutions for What is the Maxwell modifications of ampere law in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of What is the Maxwell modifications of ampere law defined & explained in the simplest way possible. Besides giving the explanation of
What is the Maxwell modifications of ampere law, a detailed solution for What is the Maxwell modifications of ampere law has been provided alongside types of What is the Maxwell modifications of ampere law theory, EduRev gives you an
ample number of questions to practice What is the Maxwell modifications of ampere law tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















