Introduction
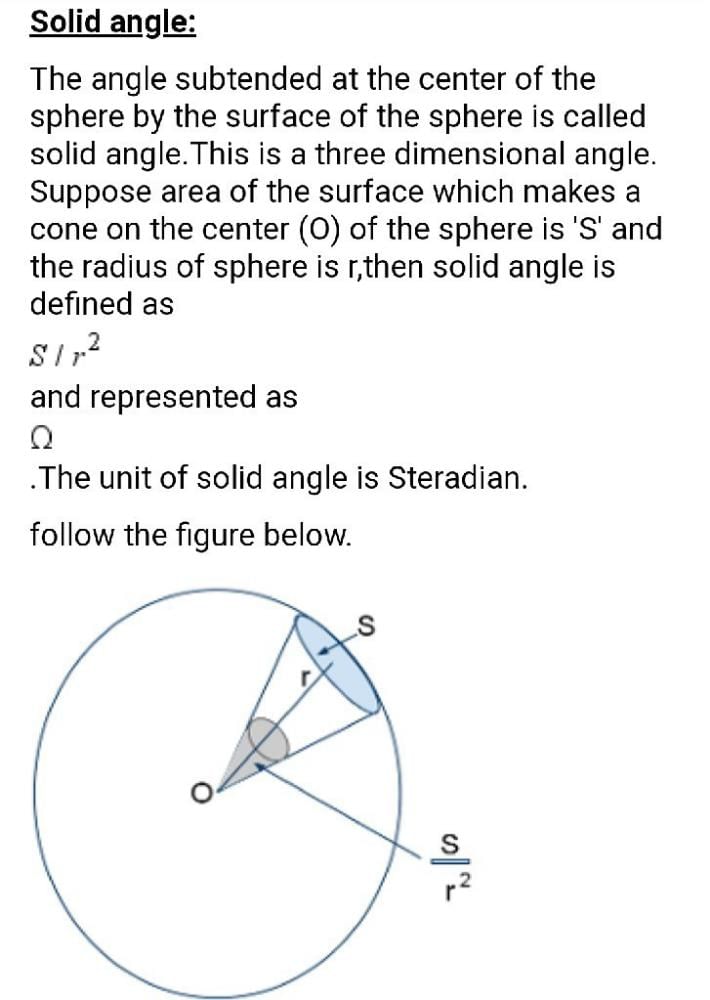
The solid angle subtended at the centre of a sphere by its whole surface is an important concept in geometry. In this concept, we consider a sphere and we want to find out the solid angle that it subtends at its centre. This is an important concept in many areas of physics, particularly in optics and electromagnetism.

Definition of Solid Angle
Solid angle is a measure of the amount of three-dimensional space that is enclosed by a surface. It is defined as the ratio of the surface area of a portion of a sphere to the square of its radius.

Formula for Solid Angle
The formula for solid angle is given by:
Ω = A / r²
where Ω is the solid angle in steradians, A is the surface area of the portion of the sphere and r is the radius of the sphere.

Calculation of Solid Angle
To calculate the solid angle subtended at the centre of a sphere by its whole surface, we need to consider the entire surface area of the sphere. The surface area of a sphere is given by:
A = 4πr²
where A is the surface area and r is the radius of the sphere.

Substituting the value of A in the formula for solid angle, we get:
Ω = (4πr²) / r²
Ω = 4π

Therefore, the solid angle subtended at the centre of a sphere by its whole surface is 4π steradians.

Conclusion
In conclusion, the solid angle subtended at the centre of a sphere by its whole surface is an important concept in geometry and physics. It is defined as the ratio of the surface area of a portion of a sphere to the square of its radius. The formula for solid angle is given by A / r². By calculating the entire surface area of the sphere and substituting it in the formula, we can determine that the solid angle subtended at the centre of a sphere by its whole surface is 4π steradians.