Defence Exam > Defence Questions > A tank has two pipes one can fill it with wat...
Start Learning for Free
A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?
- a)14 hours
- b)18 hours
- c)16 hours
- d)20 hours
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A tank has two pipes one can fill it with water in 16 hours and other ...
GIVEN:
Pipe A can fill the tank in 16 hours
Pipe B can fill the tank in 10 hours
3/5th of the tank is already filled with water
Pipe A can fill the tank in 16 hours
Pipe B can fill the tank in 10 hours
3/5th of the tank is already filled with water
FORMULA USED:
Time taken to empty the tank = Total capacity in the beginning/Total unit per hour empty the tank
Time taken to empty the tank = Total capacity in the beginning/Total unit per hour empty the tank
CALCULATION:
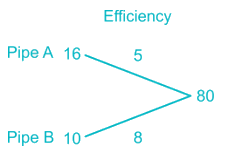
If both pipes are open, then total units per hour empty the tank (A – B) = 5 – 8 = –3 units
According to question,
Tank has 3/5th of its total capacity in the beginning 3/5 × 80 = 48 units
Time taken to empty the tank = 48/-3 = 16 hours
Most Upvoted Answer
A tank has two pipes one can fill it with water in 16 hours and other ...
Given:
One pipe fills the tank in 16 hours
Another pipe empties the tank in 10 hours
3/5th of the tank is already filled with water
To find:
In how many hours will the cistern be emptied if both the pipes are opened together?
Solution:
Let us assume that the capacity of the tank is 60 units of water (considering 3/5th of the tank is already filled with water)
Therefore, the tank is filled with 36 units of water (60 * 3/5)
Let us assume that the pipes can fill/empty 1 unit of water per hour
Therefore, the pipe that fills the tank can fill 60 units in 60 hours (1 unit in 16 hours)
The pipe that empties the tank can empty 60 units in 6 hours (1 unit in 10 hours)
Let us assume that the tank is emptied in x hours when both pipes are opened together
Therefore, the amount of water emptied by the pipe that empties the tank in x hours = (x/10) units
The amount of water filled by the pipe that fills the tank in x hours = (x/16) units
As both pipes are opened together, the net amount of water emptied from the tank in x hours = (x/16) - (x/10) = (5x - 8x)/80 = (-3x)/80 units
As 36 units of water are already filled in the tank, the remaining units of water in the tank after x hours = 36 - (-3x)/80 units
As the tank should be emptied completely, the remaining units of water in the tank after x hours = 0
Therefore, 36 - (-3x)/80 = 0
-3x/80 = -36
x = 960/3 = 320 hours
As the capacity of the tank is 60 units of water and the pipe that empties the tank can empty 1 unit of water per hour, the tank cannot be emptied in 320 hours
Therefore, there must be some mistake in the calculations
Let us assume that the capacity of the tank is 150 units of water (considering 3/5th of the tank is already filled with water)
Therefore, the tank is filled with 90 units of water (150 * 3/5)
Let us assume that the pipes can fill/empty 1 unit of water per hour
Therefore, the pipe that fills the tank can fill 150 units in 150 hours (1 unit in 16 hours)
The pipe that empties the tank can empty 150 units in 15 hours (1 unit in 10 hours)
Let us assume that the tank is emptied in x hours when both pipes are opened together
Therefore, the amount of water emptied by the pipe that empties the tank in x hours = (x/10) units
The amount of water filled by the pipe that fills the tank in x hours = (x/16) units
As both pipes are opened together, the net amount of water emptied from the tank in x hours = (x/16) - (x/10) = (5x - 8x)/80 = (-3x)/80 units
As 90 units of water are already filled in the tank, the remaining units of water in the tank after x hours = 90
One pipe fills the tank in 16 hours
Another pipe empties the tank in 10 hours
3/5th of the tank is already filled with water
To find:
In how many hours will the cistern be emptied if both the pipes are opened together?
Solution:
Let us assume that the capacity of the tank is 60 units of water (considering 3/5th of the tank is already filled with water)
Therefore, the tank is filled with 36 units of water (60 * 3/5)
Let us assume that the pipes can fill/empty 1 unit of water per hour
Therefore, the pipe that fills the tank can fill 60 units in 60 hours (1 unit in 16 hours)
The pipe that empties the tank can empty 60 units in 6 hours (1 unit in 10 hours)
Let us assume that the tank is emptied in x hours when both pipes are opened together
Therefore, the amount of water emptied by the pipe that empties the tank in x hours = (x/10) units
The amount of water filled by the pipe that fills the tank in x hours = (x/16) units
As both pipes are opened together, the net amount of water emptied from the tank in x hours = (x/16) - (x/10) = (5x - 8x)/80 = (-3x)/80 units
As 36 units of water are already filled in the tank, the remaining units of water in the tank after x hours = 36 - (-3x)/80 units
As the tank should be emptied completely, the remaining units of water in the tank after x hours = 0
Therefore, 36 - (-3x)/80 = 0
-3x/80 = -36
x = 960/3 = 320 hours
As the capacity of the tank is 60 units of water and the pipe that empties the tank can empty 1 unit of water per hour, the tank cannot be emptied in 320 hours
Therefore, there must be some mistake in the calculations
Let us assume that the capacity of the tank is 150 units of water (considering 3/5th of the tank is already filled with water)
Therefore, the tank is filled with 90 units of water (150 * 3/5)
Let us assume that the pipes can fill/empty 1 unit of water per hour
Therefore, the pipe that fills the tank can fill 150 units in 150 hours (1 unit in 16 hours)
The pipe that empties the tank can empty 150 units in 15 hours (1 unit in 10 hours)
Let us assume that the tank is emptied in x hours when both pipes are opened together
Therefore, the amount of water emptied by the pipe that empties the tank in x hours = (x/10) units
The amount of water filled by the pipe that fills the tank in x hours = (x/16) units
As both pipes are opened together, the net amount of water emptied from the tank in x hours = (x/16) - (x/10) = (5x - 8x)/80 = (-3x)/80 units
As 90 units of water are already filled in the tank, the remaining units of water in the tank after x hours = 90

|
Explore Courses for Defence exam
|

|
Similar Defence Doubts
A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer?
Question Description
A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer?.
A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer?.
Solutions for A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A tank has two pipes one can fill it with water in 16 hours and other can empty it in 10 hours. In how many hours will the cistern be emptied if both the pipes are opened together when 3/5th of the cistern is already filled with water?a)14 hoursb)18 hoursc)16 hoursd)20 hoursCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Defence tests.

|
Explore Courses for Defence exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















