Mechanical Engineering Exam > Mechanical Engineering Questions > The ratio of total emissive power of body to ...
Start Learning for Free
The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is called
- a)Absorptivity
- b)Transmissivity
- c)Reflectivity
- d)Emissivity
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
The ratio of total emissive power of body to the total emissive power ...
Emissivity for any body is given by
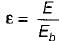
Where
E = Emissive power of a body
Eb = Emissive power of a black body
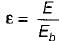
Where
E = Emissive power of a body
Eb = Emissive power of a black body
Most Upvoted Answer
The ratio of total emissive power of body to the total emissive power ...
Emissivity is the property of a material that describes its ability to emit thermal radiation. It is defined as the ratio of the total emissive power of a body to the total emissive power of a black body at the same temperature. The correct answer to the question is option 'D'.
Explanation:
1. Emissivity:
- Emissivity is a dimensionless quantity that ranges from 0 to 1.
- A value of 0 indicates that the material is a perfect reflector and does not emit any thermal radiation.
- A value of 1 indicates that the material is a perfect emitter and emits thermal radiation as a black body.
- Emissivity depends on the material's surface properties, such as roughness, composition, and temperature.
- Different materials have different emissivity values, and they can vary with wavelength and temperature.
2. Total emissive power:
- The total emissive power of a body is the total amount of thermal radiation it emits per unit area and per unit time.
- It is given by the Stefan-Boltzmann law, which states that the total emissive power is proportional to the fourth power of the absolute temperature.
- Mathematically, the total emissive power (P) is given by P = σ * A * ε * T^4, where σ is the Stefan-Boltzmann constant, A is the surface area, ε is the emissivity, and T is the absolute temperature.
3. Black body:
- A black body is an idealized object that absorbs all incident radiation without reflection or transmission.
- It is a perfect emitter of thermal radiation and has an emissivity of 1 at all wavelengths and temperatures.
- The total emissive power of a black body is given by the Stefan-Boltzmann law: P_bb = σ * A * T^4.
4. Ratio of emissive powers:
- The ratio of the total emissive power of a body to the total emissive power of a black body at the same temperature is given by P/P_bb.
- Substituting the expressions for P and P_bb, we get P/P_bb = (σ * A * ε * T^4) / (σ * A * T^4).
- The surface area and the Stefan-Boltzmann constant cancel out, leaving us with ε.
- Therefore, the ratio is equal to the emissivity of the body.
Conclusion:
The ratio of total emissive power of a body to the total emissive power of a black body at the same temperature is equal to the emissivity of the body. Hence, the correct answer is option 'D' - Emissivity.
Explanation:
1. Emissivity:
- Emissivity is a dimensionless quantity that ranges from 0 to 1.
- A value of 0 indicates that the material is a perfect reflector and does not emit any thermal radiation.
- A value of 1 indicates that the material is a perfect emitter and emits thermal radiation as a black body.
- Emissivity depends on the material's surface properties, such as roughness, composition, and temperature.
- Different materials have different emissivity values, and they can vary with wavelength and temperature.
2. Total emissive power:
- The total emissive power of a body is the total amount of thermal radiation it emits per unit area and per unit time.
- It is given by the Stefan-Boltzmann law, which states that the total emissive power is proportional to the fourth power of the absolute temperature.
- Mathematically, the total emissive power (P) is given by P = σ * A * ε * T^4, where σ is the Stefan-Boltzmann constant, A is the surface area, ε is the emissivity, and T is the absolute temperature.
3. Black body:
- A black body is an idealized object that absorbs all incident radiation without reflection or transmission.
- It is a perfect emitter of thermal radiation and has an emissivity of 1 at all wavelengths and temperatures.
- The total emissive power of a black body is given by the Stefan-Boltzmann law: P_bb = σ * A * T^4.
4. Ratio of emissive powers:
- The ratio of the total emissive power of a body to the total emissive power of a black body at the same temperature is given by P/P_bb.
- Substituting the expressions for P and P_bb, we get P/P_bb = (σ * A * ε * T^4) / (σ * A * T^4).
- The surface area and the Stefan-Boltzmann constant cancel out, leaving us with ε.
- Therefore, the ratio is equal to the emissivity of the body.
Conclusion:
The ratio of total emissive power of a body to the total emissive power of a black body at the same temperature is equal to the emissivity of the body. Hence, the correct answer is option 'D' - Emissivity.
Free Test
FREE
| Start Free Test |
Community Answer
The ratio of total emissive power of body to the total emissive power ...
Emissivity

|
Explore Courses for Mechanical Engineering exam
|

|
Question Description
The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer?.
The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is calleda)Absorptivityb)Transmissivityc)Reflectivityd)EmissivityCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























