Defence Exam > Defence Questions > In a RC phase shift oscillator, the minimum n...
Start Learning for Free
In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will be
- a)1
- b)2
- c)3
- d)4
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
In a RC phase shift oscillator, the minimum number of R-C networks to ...
RC phase shift oscillator is used to invert the input for 180° phase difference. The single R-C network gives the 60° phase shift. Hence, we need three set of R-C network which have to be connected in cascade (series). The value of R and C can be chosen by the formula, 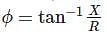
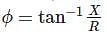
Most Upvoted Answer
In a RC phase shift oscillator, the minimum number of R-C networks to ...
RC Phase Shift Oscillator
A RC phase shift oscillator is a type of electronic oscillator that uses a combination of resistors (R) and capacitors (C) to generate a continuous sinusoidal waveform. It is a feedback oscillator circuit that produces a phase shift of 180 degrees at the desired frequency.
Minimum Number of R-C Networks
In order to generate the required phase shift of 180 degrees, a minimum of three R-C networks need to be connected in cascade.
Explanation
Here's a detailed explanation of why a minimum of three R-C networks are required for a RC phase shift oscillator:
1. Phase Shift
The phase shift in each R-C network is determined by the RC time constant. In a RC circuit, the phase shift is given by the formula:
Phase shift = arctan(1/2πfRC)
where f is the frequency and RC is the time constant.
2. Required Phase Shift
For a RC phase shift oscillator to oscillate at a particular frequency, the total phase shift around the loop must be 360 degrees or 2π radians. Since each R-C network contributes a phase shift of approximately 60 degrees (π/3 radians), a minimum of six R-C networks would be required to achieve a total phase shift of 360 degrees.
3. Feedback Loop
However, in a practical RC phase shift oscillator, the feedback loop is broken at one of the R-C networks. This is done to prevent the circuit from becoming unstable and to ensure that the output waveform is sinusoidal. Breaking the loop reduces the total phase shift by 180 degrees (π radians).
4. Total Phase Shift
With the feedback loop broken, the total phase shift required is reduced to 180 degrees. Since each R-C network contributes a phase shift of approximately 60 degrees (π/3 radians), a minimum of three R-C networks is sufficient to achieve the required total phase shift of 180 degrees.
Conclusion
In summary, a RC phase shift oscillator requires a minimum of three R-C networks connected in cascade to generate the required phase shift of 180 degrees. The combination of resistors and capacitors in these networks determines the frequency of oscillation, while the feedback loop ensures stable operation and a sinusoidal output waveform.
A RC phase shift oscillator is a type of electronic oscillator that uses a combination of resistors (R) and capacitors (C) to generate a continuous sinusoidal waveform. It is a feedback oscillator circuit that produces a phase shift of 180 degrees at the desired frequency.
Minimum Number of R-C Networks
In order to generate the required phase shift of 180 degrees, a minimum of three R-C networks need to be connected in cascade.
Explanation
Here's a detailed explanation of why a minimum of three R-C networks are required for a RC phase shift oscillator:
1. Phase Shift
The phase shift in each R-C network is determined by the RC time constant. In a RC circuit, the phase shift is given by the formula:
Phase shift = arctan(1/2πfRC)
where f is the frequency and RC is the time constant.
2. Required Phase Shift
For a RC phase shift oscillator to oscillate at a particular frequency, the total phase shift around the loop must be 360 degrees or 2π radians. Since each R-C network contributes a phase shift of approximately 60 degrees (π/3 radians), a minimum of six R-C networks would be required to achieve a total phase shift of 360 degrees.
3. Feedback Loop
However, in a practical RC phase shift oscillator, the feedback loop is broken at one of the R-C networks. This is done to prevent the circuit from becoming unstable and to ensure that the output waveform is sinusoidal. Breaking the loop reduces the total phase shift by 180 degrees (π radians).
4. Total Phase Shift
With the feedback loop broken, the total phase shift required is reduced to 180 degrees. Since each R-C network contributes a phase shift of approximately 60 degrees (π/3 radians), a minimum of three R-C networks is sufficient to achieve the required total phase shift of 180 degrees.
Conclusion
In summary, a RC phase shift oscillator requires a minimum of three R-C networks connected in cascade to generate the required phase shift of 180 degrees. The combination of resistors and capacitors in these networks determines the frequency of oscillation, while the feedback loop ensures stable operation and a sinusoidal output waveform.

|
Explore Courses for Defence exam
|

|
In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer?
Question Description
In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer?.
In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer?.
Solutions for In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer?, a detailed solution for In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice In a RC phase shift oscillator, the minimum number of R-C networks to be connected in cascade will bea)1b)2c)3d)4Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Defence tests.

|
Explore Courses for Defence exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
















