Defence Exam > Defence Questions > Consider the following statements:1) The peri...
Start Learning for Free
Consider the following statements:
1) The perimeter of a triangle is greater than the sum of its three medinas.
2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.
Which of the above statements is/are correct?
1) The perimeter of a triangle is greater than the sum of its three medinas.
2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.
Which of the above statements is/are correct?
- a)1 only
- b)2 only
- c)Both 1 and 2
- d)Neither 1 nor 2
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider the following statements:1) The perimeter of a triangle is gr...
1. Perimeter of triangle is greater than the sum of 3 medians
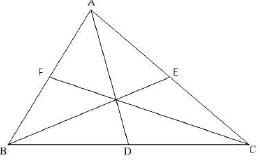
Let ABC be the triangle and D. E and F are midpoints of BC, CA and AB respectively.
Recall that the sum of two sides of a triangle is greater than twice the median bisecting the third side,(Theorem to be remembered)
Hence in ΔABD, AD is a median
⇒ AB + AC > 2(AD)
Similarly, we get
BC + AC > 2CF
BC + AB > 2BE
On adding the above inequations, we get
(AB + AC) + (BC + AC) + (BC + AB )> 2AD + 2CD + 2BE
2(AB + BC + AC) > 2(AD + BE + CF)
∴ AB + BC + AC > AD + BE + CF
2.
To prove: AB + BC + CA > 2AD
Construction: AD is joined
Proof: In triangle ABD, AB + BD > AD [because, the sum of any two sides of a triangle is always greater than the third side] ---- 1
In triangle ADC, AC + DC > AD [because, the sum of any two sides of a triangle is always greater than the third side] ---- 2
Adding 1 and 2 we get,
AB + BD + AC + DC > AD + AD
=> AB + (BD + DC) + AC > 2AD
=> AB + BC + AC > 2AD
Hence proved
Let ABC be the triangle and D. E and F are midpoints of BC, CA and AB respectively.
Recall that the sum of two sides of a triangle is greater than twice the median bisecting the third side,(Theorem to be remembered)
Hence in ΔABD, AD is a median
⇒ AB + AC > 2(AD)
Similarly, we get
BC + AC > 2CF
BC + AB > 2BE
On adding the above inequations, we get
(AB + AC) + (BC + AC) + (BC + AB )> 2AD + 2CD + 2BE
2(AB + BC + AC) > 2(AD + BE + CF)
∴ AB + BC + AC > AD + BE + CF
2.
To prove: AB + BC + CA > 2AD
Construction: AD is joined
Proof: In triangle ABD, AB + BD > AD [because, the sum of any two sides of a triangle is always greater than the third side] ---- 1
In triangle ADC, AC + DC > AD [because, the sum of any two sides of a triangle is always greater than the third side] ---- 2
Adding 1 and 2 we get,
AB + BD + AC + DC > AD + AD
=> AB + (BD + DC) + AC > 2AD
=> AB + BC + AC > 2AD
Hence proved
Most Upvoted Answer
Consider the following statements:1) The perimeter of a triangle is gr...
1. Perimeter of triangle is greater than the sum of 3 medians
Let ABC be the triangle and D. E and F are midpoints of BC, CA and AB respectively.
Recall that the sum of two sides of a triangle is greater than twice the median bisecting the third side,(Theorem to be remembered)
Hence in ΔABD, AD is a median
⇒ AB + AC > 2(AD)
Similarly, we get
BC + AC > 2CF
BC + AB > 2BE
On adding the above inequations, we get
(AB + AC) + (BC + AC) + (BC + AB )> 2AD + 2CD + 2BE
2(AB + BC + AC) > 2(AD + BE + CF)
∴ AB + BC + AC > AD + BE + CF
2.
To prove: AB + BC + CA > 2AD
Construction: AD is joined
Proof: In triangle ABD, AB + BD > AD [because, the sum of any two sides of a triangle is always greater than the third side] ---- 1
In triangle ADC, AC + DC > AD [because, the sum of any two sides of a triangle is always greater than the third side] ---- 2
Adding 1 and 2 we get,
AB + BD + AC + DC > AD + AD
=> AB + (BD + DC) + AC > 2AD
=> AB + BC + AC > 2AD
Hence proved
Let ABC be the triangle and D. E and F are midpoints of BC, CA and AB respectively.
Recall that the sum of two sides of a triangle is greater than twice the median bisecting the third side,(Theorem to be remembered)
Hence in ΔABD, AD is a median
⇒ AB + AC > 2(AD)
Similarly, we get
BC + AC > 2CF
BC + AB > 2BE
On adding the above inequations, we get
(AB + AC) + (BC + AC) + (BC + AB )> 2AD + 2CD + 2BE
2(AB + BC + AC) > 2(AD + BE + CF)
∴ AB + BC + AC > AD + BE + CF
2.
To prove: AB + BC + CA > 2AD
Construction: AD is joined
Proof: In triangle ABD, AB + BD > AD [because, the sum of any two sides of a triangle is always greater than the third side] ---- 1
In triangle ADC, AC + DC > AD [because, the sum of any two sides of a triangle is always greater than the third side] ---- 2
Adding 1 and 2 we get,
AB + BD + AC + DC > AD + AD
=> AB + (BD + DC) + AC > 2AD
=> AB + BC + AC > 2AD
Hence proved
|
Explore Courses for Defence exam
|
|
Similar Defence Doubts
Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer?
Question Description
Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer?.
Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer?.
Solutions for Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer?, a detailed solution for Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider the following statements:1) The perimeter of a triangle is greater than the sum of its three medinas.2) In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.Which of the above statements is/are correct?a)1 onlyb)2 onlyc)Both 1 and 2d)Neither 1 nor 2Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Defence tests.
|
|
Explore Courses for Defence exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup