Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > Laminar flow of a fluid of viscosity 0.90 kg...
Start Learning for Free
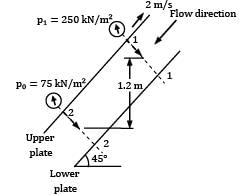
Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.
- a)0.73 N/m2and 0.691 m/s
- b)0.691 N/m2and 0.73 m/s
- c)6.91 N/m2and 7.3 m/s
- d)7.3 N/m2and 0.691 m/s
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250...
Since the plates are placed uniformly apart, velocity head would be the same at the two sections and as such flow direction will be dictated by the value of the piezometric head.


View all questions of this test
Taking a horizontal line passing through point 2 as datum Piezometric head at point 1,
p1∗ = p1 + wy1


Since p1∗ is greater that p2∗ , the direction of flow is from section 1-1 to section 2-2, i.e., downward. Apparently the upper plate is moved up the slope. Pressure gradient


Most Upvoted Answer
Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250...
Given data:
Viscosity of fluid (μ) = 0.90 kg/ms
Mass density of fluid (ρ) = 1250 kg/m3
Distance between plates (d) = 10 mm = 0.01 m
Inclination angle (θ) = 45°
Vertical distance between pressure gauges (h) = 1.2 m
Pressure at lower point (P1) = 75 kN/m2
Pressure at upper point (P2) = 250 kN/m2
Velocity of upper plate (V) = 2.0 m/s
(i) Maximum flow velocity:
To find the maximum flow velocity, we can use the Bernoulli's equation for steady, incompressible, laminar flow between plates. The equation is given as:
P1 + 0.5ρV1^2 + ρgh1 = P2 + 0.5ρV2^2 + ρgh2
Where P1 and P2 are the pressures at points 1 and 2, V1 and V2 are the velocities at points 1 and 2, and h1 and h2 are the heights at points 1 and 2.
At point 1:
P1 = 75 kN/m2 = 75,000 N/m2
V1 = 0 (since the fluid is at rest at point 1)
h1 = 0 (reference level)
At point 2:
P2 = 250 kN/m2 = 250,000 N/m2
V2 = -2.0 m/s (opposite direction to the fluid flow)
h2 = 1.2 m
Substituting these values into the Bernoulli's equation, we get:
75,000 + 0 + 0 = 250,000 + 0.5 × 1250 × Vmax^2 + 1250 × 9.81 × 1.2
Simplifying the equation, we have:
Vmax^2 = (75,000 - 250,000 + 1250 × 9.81 × 1.2) / (0.5 × 1250)
Vmax^2 = -35.78
Since velocity cannot be negative, the maximum flow velocity (Vmax) is the square root of the positive value of -35.78, which is approximately 5.99 m/s.
(ii) Shear stress on the upper plate:
To find the shear stress on the upper plate, we can use Newton's law of viscosity, which states that the shear stress (τ) is directly proportional to the velocity gradient (du/dy) and the dynamic viscosity (μ). The equation is given as:
τ = μ × (du/dy)
Where du/dy is the velocity gradient.
For laminar flow between plates, the velocity profile is linear. The velocity gradient can be calculated as:
du/dy = V/d
Where V is the velocity of the upper plate and d is the distance between the plates.
Substituting the values, we have:
du/dy = 2.0 / 0.01
du/dy = 200 m/s2
Finally, substituting the velocity gradient and dynamic viscosity into the equation for shear stress, we get:
τ =
Viscosity of fluid (μ) = 0.90 kg/ms
Mass density of fluid (ρ) = 1250 kg/m3
Distance between plates (d) = 10 mm = 0.01 m
Inclination angle (θ) = 45°
Vertical distance between pressure gauges (h) = 1.2 m
Pressure at lower point (P1) = 75 kN/m2
Pressure at upper point (P2) = 250 kN/m2
Velocity of upper plate (V) = 2.0 m/s
(i) Maximum flow velocity:
To find the maximum flow velocity, we can use the Bernoulli's equation for steady, incompressible, laminar flow between plates. The equation is given as:
P1 + 0.5ρV1^2 + ρgh1 = P2 + 0.5ρV2^2 + ρgh2
Where P1 and P2 are the pressures at points 1 and 2, V1 and V2 are the velocities at points 1 and 2, and h1 and h2 are the heights at points 1 and 2.
At point 1:
P1 = 75 kN/m2 = 75,000 N/m2
V1 = 0 (since the fluid is at rest at point 1)
h1 = 0 (reference level)
At point 2:
P2 = 250 kN/m2 = 250,000 N/m2
V2 = -2.0 m/s (opposite direction to the fluid flow)
h2 = 1.2 m
Substituting these values into the Bernoulli's equation, we get:
75,000 + 0 + 0 = 250,000 + 0.5 × 1250 × Vmax^2 + 1250 × 9.81 × 1.2
Simplifying the equation, we have:
Vmax^2 = (75,000 - 250,000 + 1250 × 9.81 × 1.2) / (0.5 × 1250)
Vmax^2 = -35.78
Since velocity cannot be negative, the maximum flow velocity (Vmax) is the square root of the positive value of -35.78, which is approximately 5.99 m/s.
(ii) Shear stress on the upper plate:
To find the shear stress on the upper plate, we can use Newton's law of viscosity, which states that the shear stress (τ) is directly proportional to the velocity gradient (du/dy) and the dynamic viscosity (μ). The equation is given as:
τ = μ × (du/dy)
Where du/dy is the velocity gradient.
For laminar flow between plates, the velocity profile is linear. The velocity gradient can be calculated as:
du/dy = V/d
Where V is the velocity of the upper plate and d is the distance between the plates.
Substituting the values, we have:
du/dy = 2.0 / 0.01
du/dy = 200 m/s2
Finally, substituting the velocity gradient and dynamic viscosity into the equation for shear stress, we get:
τ =
Attention Civil Engineering (CE) Students!
To make sure you are not studying endlessly, EduRev has designed Civil Engineering (CE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Civil Engineering (CE).

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer?
Question Description
Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer?.
Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.a) 0.73 N/m2and 0.691 m/sb) 0.691 N/m2and 0.73 m/sc) 6.91 N/m2and 7.3 m/sd) 7.3 N/m2and 0.691 m/sCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























