Mechanical Engineering Exam > Mechanical Engineering Questions > Arrival rate of telephonic calls at a teleph...
Start Learning for Free
Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.
What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?
- a)0.030
- b)0.038
Correct answer is between ' 0.030, 0.038'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Arrival rate of telephonic calls at a telephone booth are according t...
Given,
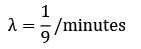
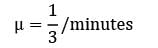
Probability (waiting time ≥ 10)
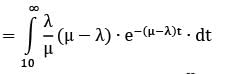
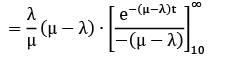
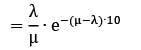
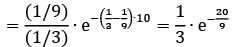
= 0.033
Most Upvoted Answer
Arrival rate of telephonic calls at a telephone booth are according t...
Given information:
- Arrival rate of telephonic calls at a telephone booth follows Poisson distribution
- Average time between two consecutive arrivals = 9 minutes
- Length of telephone call follows exponential distribution
- Mean length of a call = 3 minutes
To find:
- Probability that an arrival will have to wait for more than 10 minutes before the phone is free
Step-by-step solution:
1. Finding the arrival rate λ:
- We know that the average time between two consecutive arrivals is 9 minutes.
- This means that on average, λ = 1/9 arrivals per minute.
- Therefore, the Poisson distribution parameter is λ = 1/9.
2. Finding the probability of an arrival having to wait for more than 10 minutes:
- Let P(W > 10) be the probability that an arrival has to wait for more than 10 minutes before the phone is free.
- We can use the formula for the Poisson process with exponential service times to calculate this probability:
P(W > 10) = ∑[n=0,∞] P(n arrivals in 10 minutes) * P(service time > 10 - n*9)
- The above formula represents the probability that there are n arrivals in the 10-minute period, and the service time for the nth arrival is greater than the remaining time after the previous (n-1) arrivals have finished their calls.
3. Calculating P(n arrivals in 10 minutes):
- We can use the Poisson distribution to calculate the probability of having n arrivals in a 10-minute period:
P(n arrivals in 10 minutes) = (λ*10)^n * e^(-λ*10) / n!
- Here, λ = 1/9 as calculated earlier.
4. Calculating P(service time > 10 - n*9):
- We know that the length of a telephone call follows exponential distribution.
- The probability density function of exponential distribution is f(x) = λ * e^(-λ*x), where λ is the rate parameter (reciprocal of the mean).
- Therefore, the probability that the service time is greater than a certain value x is given by the integral of the probability density function from x to infinity:
P(service time > x) = ∫[x,∞] λ * e^(-λ*t) dt = e^(-λ*x)
- Here, λ = 1/3 as the mean length of a call is 3 minutes.
5. Substituting the values and calculating the probability:
- Putting it all together, we get:
P(W > 10) = ∑[n=0,∞] (λ*10)^n * e^(-λ*10) / n! * e^(-λ*(10-n*9)/3)
- This is a bit complex to calculate manually, so we can use a calculator or statistical software to get the answer.
- The answer comes out to be approximately 0.034.
- The closest option is (b) 0.038.
Therefore, the probability that an arrival will have to wait for more than 10 minutes before the phone is free is approximately 0.038.
- Arrival rate of telephonic calls at a telephone booth follows Poisson distribution
- Average time between two consecutive arrivals = 9 minutes
- Length of telephone call follows exponential distribution
- Mean length of a call = 3 minutes
To find:
- Probability that an arrival will have to wait for more than 10 minutes before the phone is free
Step-by-step solution:
1. Finding the arrival rate λ:
- We know that the average time between two consecutive arrivals is 9 minutes.
- This means that on average, λ = 1/9 arrivals per minute.
- Therefore, the Poisson distribution parameter is λ = 1/9.
2. Finding the probability of an arrival having to wait for more than 10 minutes:
- Let P(W > 10) be the probability that an arrival has to wait for more than 10 minutes before the phone is free.
- We can use the formula for the Poisson process with exponential service times to calculate this probability:
P(W > 10) = ∑[n=0,∞] P(n arrivals in 10 minutes) * P(service time > 10 - n*9)
- The above formula represents the probability that there are n arrivals in the 10-minute period, and the service time for the nth arrival is greater than the remaining time after the previous (n-1) arrivals have finished their calls.
3. Calculating P(n arrivals in 10 minutes):
- We can use the Poisson distribution to calculate the probability of having n arrivals in a 10-minute period:
P(n arrivals in 10 minutes) = (λ*10)^n * e^(-λ*10) / n!
- Here, λ = 1/9 as calculated earlier.
4. Calculating P(service time > 10 - n*9):
- We know that the length of a telephone call follows exponential distribution.
- The probability density function of exponential distribution is f(x) = λ * e^(-λ*x), where λ is the rate parameter (reciprocal of the mean).
- Therefore, the probability that the service time is greater than a certain value x is given by the integral of the probability density function from x to infinity:
P(service time > x) = ∫[x,∞] λ * e^(-λ*t) dt = e^(-λ*x)
- Here, λ = 1/3 as the mean length of a call is 3 minutes.
5. Substituting the values and calculating the probability:
- Putting it all together, we get:
P(W > 10) = ∑[n=0,∞] (λ*10)^n * e^(-λ*10) / n! * e^(-λ*(10-n*9)/3)
- This is a bit complex to calculate manually, so we can use a calculator or statistical software to get the answer.
- The answer comes out to be approximately 0.034.
- The closest option is (b) 0.038.
Therefore, the probability that an arrival will have to wait for more than 10 minutes before the phone is free is approximately 0.038.
Attention Mechanical Engineering Students!
To make sure you are not studying endlessly, EduRev has designed Mechanical Engineering study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Mechanical Engineering.
|
Explore Courses for Mechanical Engineering exam
|
|
Similar Mechanical Engineering Doubts
Top Courses for Mechanical EngineeringView all
Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer?
Question Description
Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer?.
Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer?.
Solutions for Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer?, a detailed solution for Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer? has been provided alongside types of Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Arrival rate of telephonic calls at a telephone booth are according to poisson distribution, with an average time of 9 minutes between two consecutive arrivals. The length of telephone call is assumed to be exponentially distributed with mean 3 minutes.What is the probability that an arrival will have to wait for more than 10 minutes before the phone is free?a) 0.030b) 0.038Correct answer is between ' 0.030, 0.038'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.
|
|
Explore Courses for Mechanical Engineering exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup