Defence Exam > Defence Questions > There are two parallel streets each directed ...
Start Learning for Free
There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?
- a)7.5 km
- b)10.5 km
- c)12.5 km
- d)15 km
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
There are two parallel streets each directed north to south. A person ...
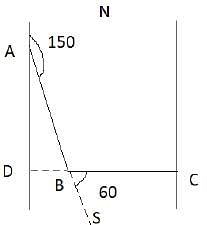
Initially the person is travelling from south to north i.e. D to A
He takes 150o right turn and moves AB distance and then he takes 60o left turn travels BC
AB = 20km/hr * 15/60 hr = 5km
BC = 30 * 20/60 = 10 km
We know that distance between both the streets is DC = DB + BC
DB = AB cos 60o = 5. ½ = 2.5 km
So the distance between streets = 12.5 km
 This question is part of UPSC exam. View all Defence courses
This question is part of UPSC exam. View all Defence courses
Most Upvoted Answer
There are two parallel streets each directed north to south. A person ...
Distance between the two streets
Given information:
- Two parallel streets, both directed north to south.
- A person in the first street is traveling from south to north.
- The person wants to take the second street which is on his right side.
- The person makes a 150° turn to the right and travels for 15 minutes at a speed of 20 km/hr.
- Then, the person takes a left turn of 60° and travels for 20 minutes at a speed of 30 km/hr in order to meet the second street.
To find the distance between the two streets, we can break down the person's movements into vectors and use trigonometry to find the distance.
Calculating the first vector:
- The person makes a 150° turn to the right and travels for 15 minutes at a speed of 20 km/hr.
- The distance covered in this vector can be calculated using the formula: distance = speed × time.
- Therefore, the distance covered in this vector is 20 km/hr × (15/60) hr = 5 km.
Calculating the second vector:
- The person takes a left turn of 60° and travels for 20 minutes at a speed of 30 km/hr.
- Again, using the formula distance = speed × time, the distance covered in this vector is 30 km/hr × (20/60) hr = 10 km.
Calculating the resultant vector:
- The resultant vector is the vector formed by adding the two vectors calculated above.
- This can be done using the cosine rule: c² = a² + b² - 2abcos(C), where c is the magnitude of the resultant vector, a and b are the magnitudes of the individual vectors, and C is the angle between them.
- Plugging in the values, we have: c² = 5² + 10² - 2(5)(10)cos(150°).
- Solving this equation gives us: c ≈ 12.5 km.
Therefore, the distance between the two streets is approximately 12.5 km.
Hence, the correct answer is option C.
Given information:
- Two parallel streets, both directed north to south.
- A person in the first street is traveling from south to north.
- The person wants to take the second street which is on his right side.
- The person makes a 150° turn to the right and travels for 15 minutes at a speed of 20 km/hr.
- Then, the person takes a left turn of 60° and travels for 20 minutes at a speed of 30 km/hr in order to meet the second street.
To find the distance between the two streets, we can break down the person's movements into vectors and use trigonometry to find the distance.
Calculating the first vector:
- The person makes a 150° turn to the right and travels for 15 minutes at a speed of 20 km/hr.
- The distance covered in this vector can be calculated using the formula: distance = speed × time.
- Therefore, the distance covered in this vector is 20 km/hr × (15/60) hr = 5 km.
Calculating the second vector:
- The person takes a left turn of 60° and travels for 20 minutes at a speed of 30 km/hr.
- Again, using the formula distance = speed × time, the distance covered in this vector is 30 km/hr × (20/60) hr = 10 km.
Calculating the resultant vector:
- The resultant vector is the vector formed by adding the two vectors calculated above.
- This can be done using the cosine rule: c² = a² + b² - 2abcos(C), where c is the magnitude of the resultant vector, a and b are the magnitudes of the individual vectors, and C is the angle between them.
- Plugging in the values, we have: c² = 5² + 10² - 2(5)(10)cos(150°).
- Solving this equation gives us: c ≈ 12.5 km.
Therefore, the distance between the two streets is approximately 12.5 km.
Hence, the correct answer is option C.
Community Answer
There are two parallel streets each directed north to south. A person ...

Initially the person is travelling from south to north i.e. D to A
He takes 150o right turn and moves AB distance and then he takes 60o left turn travels BC
AB = 20km/hr * 15/60 hr = 5km
BC = 30 * 20/60 = 10 km
We know that distance between both the streets is DC = DB + BC
DB = AB cos 60o = 5. ½ = 2.5 km
So the distance between streets = 12.5 km

|
Explore Courses for Defence exam
|

|
Similar Defence Doubts
There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer?
Question Description
There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer?.
There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer?.
Solutions for There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice There are two parallel streets each directed north to south. A person in the first street travelling from south to north wishes to take the second street which is on his right side. At some place, he makes a 150o turn to the right and he travels for 15 minutes at the speed of 20 km/hr. After that he takes a left turn of 60o and travels for 20 minutes at the speed of 30 km/hr in order to meet the second street. What is the distance between the two streets?a)7.5 kmb)10.5 kmc)12.5 kmd)15 kmCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Defence tests.

|
Explore Courses for Defence exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















