All Courses
Explore Courses UPSC Exam UPSC Test Series Free Notes EduRev Infinity Get the App Login Join for Free
Sign in Open App
Class 12 Exam  >  Class 12 Questions  >  Calculate the refractive index of the materia... Start Learning for Free
SaveJoin the Discussion on the App
Calculate the refractive index of the material of an equilateral prism for which the angle of minimum deviation is 60°.
  • a)
    √3/2
  • b)
    √3
  • c)
    1/2
  • d)
    1/√2
Correct answer is option 'B'. Can you explain this answer?
FREE This question is part of
Download PDF Attempt Test
Download PDF Attempt this Test
Most Upvoted Answer
Calculate the refractive index of the material of an equilateral prism...
Refractive index of the prism material is μ =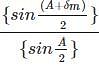 

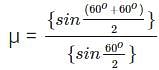
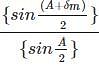
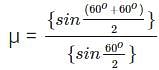
μ = √3.
Free Test
FREE
Start Free Test
Start Free Test
Community Answer
Calculate the refractive index of the material of an equilateral prism...
The angle of minimum deviation (Dm) for an equilateral prism is given by the relation:

Dm = A + (μ - 1) * A

where A is the angle of the prism and μ is the refractive index of the prism material.

In this case, the angle of the prism A is 60 degrees, and we want to find the refractive index μ.

Substituting the given values into the equation:

60 = 60 + (μ - 1) * 60

Simplifying the equation:

0 = (μ - 1) * 60

Since the angle of minimum deviation is 60 degrees, the equation simplifies to:

0 = μ - 1

Solving for μ:

μ = 1

Therefore, the refractive index of the material of the equilateral prism is 1.
< Previous Question Next Question >
Explore Courses for Class 12 exam

Similar Class 12 Doubts

Read the following text and answer the following questions on the basis of the same:Negative Refractive Index: One of the most fundamental phenomena in optics is refraction. When a beam of light crosses the interface between two different materials, its path is altered depending on the difference in the refractive indices of the materials. The greater the difference, the greater the refraction of the beam. For all known naturally occurring materials the refractive index assumes only positive values. But does this have to be the case?In 1967, Soviet physicist Victor Veselago hypothesized that a material with a negative refractive index could exist without violating any of the laws of physics.Veselago predicted that this remarkable material would exhibit a wide variety of new optical phenomena. However, until recently no one had found such a material and Veselago’s ideas had remained untested. Recently, meta-material samples are being tested for negative refractive index. But the experiments show significant losses and this could be an intrinsic property of negativeindex materials.Snell’s law is satisfied for the materials having a negative refractive index, but the direction of the refracted light ray is ‘mirror-imaged’ about the normal to the surface.There will be an interesting difference in image formation if a vessel is filled with “negative water” having refractive index – 1.33 instead of regular water having refractive index 1.33.Say, there is a fish in a vessel filled with negative water. The position of the fish is such that the observer cannot see it due to normal refraction since the refracted ray does not reach to his eye.But due to negative refraction, he will be able to see it since the refracted ray now reaches his eye.Q. A ray incident on normal glass and “negative glass” at an angle 60°. If the magnitude of angle of refraction in normal glass is 45° then, what will be the magnitude of angle of refraction in the “negative glass”?

Read the following text and answer the following questions on the basis of the same:Negative Refractive Index: One of the most fundamental phenomena in optics is refraction. When a beam of light crosses the interface between two different materials, its path is altered depending on the difference in the refractive indices of the materials. The greater the difference, the greater the refraction of the beam. For all known naturally occurring materials the refractive index assumes only positive values. But does this have to be the case?In 1967, Soviet physicist Victor Veselago hypothesized that a material with a negative refractive index could exist without violating any of the laws of physics.Veselago predicted that this remarkable material would exhibit a wide variety of new optical phenomena. However, until recently no one had found such a material and Veselago’s ideas had remained untested. Recently, meta-material samples are being tested for negative refractive index. But the experiments show significant losses and this could be an intrinsic property of negativeindex materials.Snell’s law is satisfied for the materials having a negative refractive index, but the direction of the refracted light ray is ‘mirror-imaged’ about the normal to the surface.There will be an interesting difference in image formation if a vessel is filled with “negative water” having refractive index – 1.33 instead of regular water having refractive index 1.33.Say, there is a fish in a vessel filled with negative water. The position of the fish is such that the observer cannot see it due to normal refraction since the refracted ray does not reach to his eye.But due to negative refraction, he will be able to see it since the refracted ray now reaches his eye.Q. When the angle of incidence will be equal to angle of refraction for material having negative refraction index?

Calculate the refractive index of the material of an equilateral prism for which the angle of minimum deviation is 60°.a)√3/2b)√3c)1/2d)1/√2Correct answer is option 'B'. Can you explain this answer?
Question Description
Calculate the refractive index of the material of an equilateral prism for which the angle of minimum deviation is 60°.a)√3/2b)√3c)1/2d)1/√2Correct answer is option 'B'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Calculate the refractive index of the material of an equilateral prism for which the angle of minimum deviation is 60°.a)√3/2b)√3c)1/2d)1/√2Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Calculate the refractive index of the material of an equilateral prism for which the angle of minimum deviation is 60°.a)√3/2b)√3c)1/2d)1/√2Correct answer is option 'B'. Can you explain this answer?.
Solutions for Calculate the refractive index of the material of an equilateral prism for which the angle of minimum deviation is 60°.a)√3/2b)√3c)1/2d)1/√2Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12. Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Calculate the refractive index of the material of an equilateral prism for which the angle of minimum deviation is 60°.a)√3/2b)√3c)1/2d)1/√2Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of Calculate the refractive index of the material of an equilateral prism for which the angle of minimum deviation is 60°.a)√3/2b)√3c)1/2d)1/√2Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Calculate the refractive index of the material of an equilateral prism for which the angle of minimum deviation is 60°.a)√3/2b)√3c)1/2d)1/√2Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Calculate the refractive index of the material of an equilateral prism for which the angle of minimum deviation is 60°.a)√3/2b)√3c)1/2d)1/√2Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an ample number of questions to practice Calculate the refractive index of the material of an equilateral prism for which the angle of minimum deviation is 60°.a)√3/2b)√3c)1/2d)1/√2Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Class 12 tests.
Explore Courses for Class 12 exam
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Get App
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup