Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > The shape of the cumulative distribution fun...
Start Learning for Free
The shape of the cumulative distribution function of Gaussian distribution is:
- a)Straight line at 45 degrees angle
- b)Bell-shaped
- c)S-shaped
- d)Horizontal line
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
The shape of the cumulative distribution function of Gaussian distrib...
The image below shows a Normal Distribution Curve, and a Cumulative Distribution of that Normal (Gaussian) Distribution.
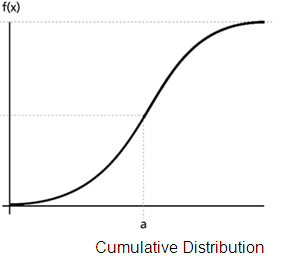


Cumulative Distribution of a Normal Distribution Curve
Free Test
FREE
| Start Free Test |
Community Answer
The shape of the cumulative distribution function of Gaussian distrib...
The shape of the cumulative distribution function of Gaussian distribution is S-shaped.
The cumulative distribution function (CDF) of a Gaussian distribution, also known as a normal distribution, is a mathematical function that describes the probability of a random variable taking on a value less than or equal to a given value. The CDF is a function of the standard deviation and mean of the distribution.
Properties of the CDF of a Gaussian Distribution:
- The CDF of a Gaussian distribution is a continuous function that ranges from 0 to 1.
- The CDF is symmetric around the mean of the distribution.
- The CDF is S-shaped, meaning it starts from a low value, gradually increases, and then levels off as it approaches 1.
Explanation:
- A straight line at a 45 degrees angle (option 'a') does not describe the shape of the CDF of a Gaussian distribution. The CDF is not a linear function and does not increase at a constant rate.
- A horizontal line (option 'd') also does not describe the shape of the CDF. A horizontal line would indicate that the probability of the random variable being less than or equal to any value is constant, which is not the case for a Gaussian distribution.
- Bell-shaped (option 'b') describes the shape of the probability density function (PDF) of a Gaussian distribution, not the CDF. The PDF represents the relative likelihood of different outcomes, while the CDF represents the cumulative probability up to a certain value.
- The correct answer is option 'c', S-shaped. The CDF of a Gaussian distribution starts from a low value, gradually increases as the value of the random variable increases, and then levels off as it approaches 1. This S-shaped curve is characteristic of the CDF of a Gaussian distribution.
In summary, the shape of the cumulative distribution function of a Gaussian distribution is S-shaped, gradually increasing from a low value to 1 as the value of the random variable increases.
The cumulative distribution function (CDF) of a Gaussian distribution, also known as a normal distribution, is a mathematical function that describes the probability of a random variable taking on a value less than or equal to a given value. The CDF is a function of the standard deviation and mean of the distribution.
Properties of the CDF of a Gaussian Distribution:
- The CDF of a Gaussian distribution is a continuous function that ranges from 0 to 1.
- The CDF is symmetric around the mean of the distribution.
- The CDF is S-shaped, meaning it starts from a low value, gradually increases, and then levels off as it approaches 1.
Explanation:
- A straight line at a 45 degrees angle (option 'a') does not describe the shape of the CDF of a Gaussian distribution. The CDF is not a linear function and does not increase at a constant rate.
- A horizontal line (option 'd') also does not describe the shape of the CDF. A horizontal line would indicate that the probability of the random variable being less than or equal to any value is constant, which is not the case for a Gaussian distribution.
- Bell-shaped (option 'b') describes the shape of the probability density function (PDF) of a Gaussian distribution, not the CDF. The PDF represents the relative likelihood of different outcomes, while the CDF represents the cumulative probability up to a certain value.
- The correct answer is option 'c', S-shaped. The CDF of a Gaussian distribution starts from a low value, gradually increases as the value of the random variable increases, and then levels off as it approaches 1. This S-shaped curve is characteristic of the CDF of a Gaussian distribution.
In summary, the shape of the cumulative distribution function of a Gaussian distribution is S-shaped, gradually increasing from a low value to 1 as the value of the random variable increases.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Question Description
The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer?.
The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer?.
Solutions for The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The shape of the cumulative distribution function of Gaussian distribution is:a)Straight line at 45 degrees angleb)Bell-shapedc)S-shapedd)Horizontal lineCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























