JEE Exam > JEE Questions > Spin-only magnetic moment of an octahedral co...
Start Learning for Free
Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. is
- a)4.89
- b)0
- c)2.82
- d)3.46
Correct answer is option 'B'. Can you explain this answer?
Most Upvoted Answer
Spin-only magnetic moment of an octahedral complex of Fe2+ in the pres...
Free Test
FREE
| Start Free Test |
Community Answer
Spin-only magnetic moment of an octahedral complex of Fe2+ in the pres...
Understanding the Spin-Only Magnetic Moment
The spin-only magnetic moment is an important concept in coordination chemistry, particularly for transition metal complexes. It is calculated using the formula:
μ = √(n(n + 2)),
where n = number of unpaired electrons.
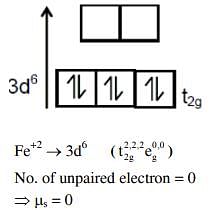
Fe2+ in an Octahedral Complex
- Iron (Fe) has an atomic number of 26, and in its +2 oxidation state, Fe2+ has the electronic configuration of [Ar] 3d^6.
- In an octahedral field, the 3d orbitals split into two sets: t2g (lower energy) and eg (higher energy).
Strong Field Ligands
- Strong field ligands, such as CN- or CO, cause a significant splitting of the d-orbitals and promote pairing of electrons.
- In the case of Fe2+ with a strong field ligand, the six d-electrons (3d^6) will fill the t2g orbitals first, resulting in:
- t2g: 6 electrons (3 pairs)
- eg: 0 electrons
This leads to no unpaired electrons.
Calculating the Spin-Only Magnetic Moment
- Since all the electrons are paired in the t2g orbitals, n (the number of unpaired electrons) is 0.
- Substituting n = 0 into the formula for magnetic moment:
μ = √(0(0 + 2)) = 0
Conclusion
Thus, the spin-only magnetic moment of the octahedral complex of Fe2+ in the presence of a strong field ligand is 0 B.M. Therefore, the correct answer is option 'B'.
The spin-only magnetic moment is an important concept in coordination chemistry, particularly for transition metal complexes. It is calculated using the formula:
μ = √(n(n + 2)),
where n = number of unpaired electrons.
Fe2+ in an Octahedral Complex
- Iron (Fe) has an atomic number of 26, and in its +2 oxidation state, Fe2+ has the electronic configuration of [Ar] 3d^6.
- In an octahedral field, the 3d orbitals split into two sets: t2g (lower energy) and eg (higher energy).
Strong Field Ligands
- Strong field ligands, such as CN- or CO, cause a significant splitting of the d-orbitals and promote pairing of electrons.
- In the case of Fe2+ with a strong field ligand, the six d-electrons (3d^6) will fill the t2g orbitals first, resulting in:
- t2g: 6 electrons (3 pairs)
- eg: 0 electrons
This leads to no unpaired electrons.
Calculating the Spin-Only Magnetic Moment
- Since all the electrons are paired in the t2g orbitals, n (the number of unpaired electrons) is 0.
- Substituting n = 0 into the formula for magnetic moment:
μ = √(0(0 + 2)) = 0
Conclusion
Thus, the spin-only magnetic moment of the octahedral complex of Fe2+ in the presence of a strong field ligand is 0 B.M. Therefore, the correct answer is option 'B'.

|
Explore Courses for JEE exam
|

|
Similar JEE Doubts
Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer?
Question Description
Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer?.
Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer?.
Solutions for Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Spin-only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in B.M. isa)4.89b)0c)2.82d)3.46Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























