Mechanical Engineering Exam > Mechanical Engineering Questions > A ball of 2 kg is dropped from a height of 15...
Start Learning for Free
A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)
Correct answer is '10'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffn...
When the ball falls through a height h on spring as shown in figure, then its potential energy is transferred to compress the spring. If compression in spring is x then total potential energy due to height h + x.
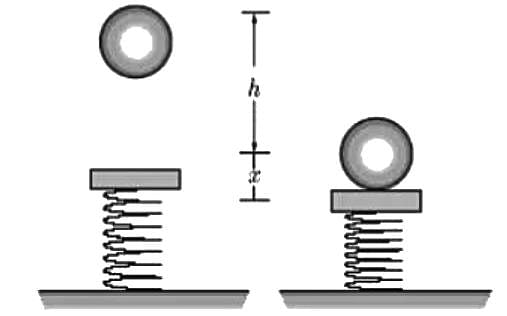
Thus
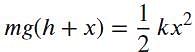
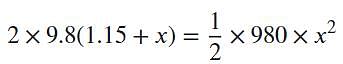
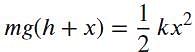
Thus substituting the values
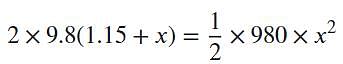
Or 0.15 + x = 25x
2
Or x
2
- 0.04x - 0.006 = 0
x = 0.1 m
x = 10 cm
Free Test
FREE
| Start Free Test |
Community Answer
A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffn...
Given data:
- Mass of the ball, m = 2 kg
- Height from which the ball is dropped, h = 15 cm = 0.15 m
- Stiffness of the spring, k = 980 N/m
Calculation:
Step 1: Potential Energy:
- The potential energy of the ball at the height h is given by the formula: PE = mgh
- Substituting the given values: PE = 2 kg * 9.8 m/s^2 * 0.15 m = 2.94 J
Step 2: Maximum Potential Energy Conversion:
- When the ball is dropped, its potential energy is converted into the maximum potential energy stored in the spring.
- The maximum potential energy stored in the spring is given by the formula: PE = (1/2) * k * x^2
- Where x is the maximum deflection of the spring.
- Rearranging the formula, we get: x = sqrt((2 * PE) / k)
- Substituting the values of PE and k: x = sqrt((2 * 2.94 J) / 980 N/m) = 0.18 m
Step 3: Conversion to Centimeters:
- Converting the maximum deflection from meters to centimeters, we get: x = 0.18 m * 100 cm/m = 18 cm
Step 4: Rounding to the Nearest Integer:
- Rounding the maximum deflection to the nearest integer, we get: x ≈ 18 cm ≈ 10 cm (rounded to the nearest integer)
Therefore, the maximum deflection in the spring is approximately 10 cm.
- Mass of the ball, m = 2 kg
- Height from which the ball is dropped, h = 15 cm = 0.15 m
- Stiffness of the spring, k = 980 N/m
Calculation:
Step 1: Potential Energy:
- The potential energy of the ball at the height h is given by the formula: PE = mgh
- Substituting the given values: PE = 2 kg * 9.8 m/s^2 * 0.15 m = 2.94 J
Step 2: Maximum Potential Energy Conversion:
- When the ball is dropped, its potential energy is converted into the maximum potential energy stored in the spring.
- The maximum potential energy stored in the spring is given by the formula: PE = (1/2) * k * x^2
- Where x is the maximum deflection of the spring.
- Rearranging the formula, we get: x = sqrt((2 * PE) / k)
- Substituting the values of PE and k: x = sqrt((2 * 2.94 J) / 980 N/m) = 0.18 m
Step 3: Conversion to Centimeters:
- Converting the maximum deflection from meters to centimeters, we get: x = 0.18 m * 100 cm/m = 18 cm
Step 4: Rounding to the Nearest Integer:
- Rounding the maximum deflection to the nearest integer, we get: x ≈ 18 cm ≈ 10 cm (rounded to the nearest integer)
Therefore, the maximum deflection in the spring is approximately 10 cm.
Attention Mechanical Engineering Students!
To make sure you are not studying endlessly, EduRev has designed Mechanical Engineering study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Mechanical Engineering.
|
Explore Courses for Mechanical Engineering exam
|
|
Similar Mechanical Engineering Doubts
Top Courses for Mechanical EngineeringView all
A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer?
Question Description
A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer?.
A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer?.
Solutions for A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer?, a detailed solution for A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer? has been provided alongside types of A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A ball of 2 kg is dropped from a height of 15 cm on a spring of stiffness k = 980 N/m. What will be the maximum deflection (in cm) in the spring? (Answer up to the nearest integer)Correct answer is '10'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.
|
|
Explore Courses for Mechanical Engineering exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup