CAT Exam > CAT Questions > Directions: Read the given information carefu...
Start Learning for Free
Directions: Read the given information carefully and answer the question that follows.
The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor club's manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.
The following diagram shows the club doors (B–1 to B–5) and the competitor club's buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.
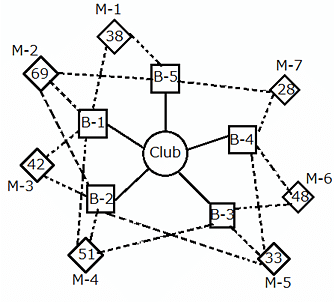
Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.
The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor club's manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.
The following diagram shows the club doors (B–1 to B–5) and the competitor club's buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.

Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.
What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?
- a)695
- b)771
- c)778
- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?

|
Explore Courses for CAT exam
|

|
Similar CAT Doubts
Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer?
Question Description
Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer?.
Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer?.
Solutions for Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Directions: Read the given information carefully and answer the question that follows.The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor clubs manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.The following diagram shows the club doors (B–1 to B–5) and the competitor clubs buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?a)695b)771c)778d)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice CAT tests.

|
Explore Courses for CAT exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























