JEE Exam > JEE Questions > The differential equation(3x + 4y + 1)dx + (4...
Start Learning for Free
The differential equation (3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family of
- a)circles
- b)parabolas
- c)ellipses
- d)hyperbolas
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represe...
The given differential equation is
(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 ...(i)
Comparing equation (i) with Mdx + Ndy = 0, we get M = 3x + 4y + 1 and N = 4x + 5y + 1.
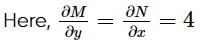
Hence, equation (i) is an exact differential equation and solution is given by
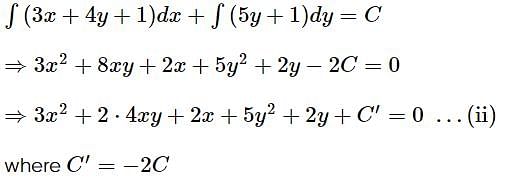
On comparing equation (ii)ii with standard form of conic section
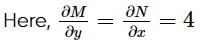
Hence, equation (i) is an exact differential equation and solution is given by
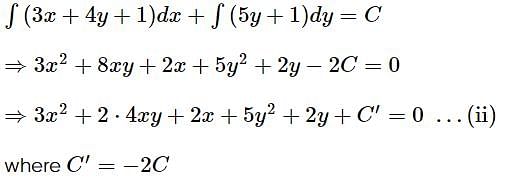
On comparing equation (ii)ii with standard form of conic section
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
we get,
a = 3, h = 4, b = 5
Here, h2 − ab = 16 − 15 = 1 > 0
Hence, the solution of differential equation represents family of hyperbolas.
Free Test
FREE
| Start Free Test |
Community Answer
The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represe...
Given differential equation: (3x + 4y + 1)dx + (4x + 5y + 1)dy = 0
To determine the family of curves represented by this differential equation, we can try to simplify it and then analyze the resulting equation.
We can start by rearranging the equation to isolate dy/dx:
(4x + 5y + 1)dy = -(3x + 4y + 1)dx
dy/dx = -(3x + 4y + 1)/(4x + 5y + 1)
To further simplify the equation, let's define a new variable u = 3x + 4y + 1 and v = 4x + 5y + 1. Taking the derivatives with respect to x, we have du/dx = 3 + 4(dy/dx) and dv/dx = 4 + 5(dy/dx).
Substituting these values back into the equation dy/dx = -(3x + 4y + 1)/(4x + 5y + 1), we get:
du/dx - 3 = -u/v
du/v - dv/u = 3
This is a homogeneous differential equation, which can be solved by substituting u = v*y and v = u*x. Taking the derivatives, we have du = v*dy + y*dv and dv = u*dx + x*du.
Substituting these values back into the equation du/v - dv/u = 3, we get:
(v*dy + y*dv)/v - (u*dx + x*du)/u = 3
dy - dx = 3
Integrating both sides, we obtain y - x = 3x + C, where C is the constant of integration.
Simplifying this equation, we get y = 4x + C.
The resulting equation y = 4x + C represents a family of straight lines. Therefore, option D, hyperbolas, is incorrect.
The correct answer is option B, parabolas, as the given differential equation represents a family of parabolas.
To determine the family of curves represented by this differential equation, we can try to simplify it and then analyze the resulting equation.
We can start by rearranging the equation to isolate dy/dx:
(4x + 5y + 1)dy = -(3x + 4y + 1)dx
dy/dx = -(3x + 4y + 1)/(4x + 5y + 1)
To further simplify the equation, let's define a new variable u = 3x + 4y + 1 and v = 4x + 5y + 1. Taking the derivatives with respect to x, we have du/dx = 3 + 4(dy/dx) and dv/dx = 4 + 5(dy/dx).
Substituting these values back into the equation dy/dx = -(3x + 4y + 1)/(4x + 5y + 1), we get:
du/dx - 3 = -u/v
du/v - dv/u = 3
This is a homogeneous differential equation, which can be solved by substituting u = v*y and v = u*x. Taking the derivatives, we have du = v*dy + y*dv and dv = u*dx + x*du.
Substituting these values back into the equation du/v - dv/u = 3, we get:
(v*dy + y*dv)/v - (u*dx + x*du)/u = 3
dy - dx = 3
Integrating both sides, we obtain y - x = 3x + C, where C is the constant of integration.
Simplifying this equation, we get y = 4x + C.
The resulting equation y = 4x + C represents a family of straight lines. Therefore, option D, hyperbolas, is incorrect.
The correct answer is option B, parabolas, as the given differential equation represents a family of parabolas.
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.
|
Explore Courses for JEE exam
|
|
Similar JEE Doubts
Top Courses for JEEView all
The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer?
Question Description
The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer?.
The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The differential equation(3x + 4y + 1)dx + (4x + 5y + 1)dy = 0 represents a family ofa)circlesb)parabolasc)ellipsesd)hyperbolasCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice JEE tests.
|
|
Explore Courses for JEE exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup