Banking Exams Exam > Banking Exams Questions > Direction: Read the following data carefully ...
Start Learning for Free
Direction: Read the following data carefully and answer the questions that follow: -
A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.
A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.
Q. What is the total number of candidates, who were not able to score more than 60% in graduation?
- a)75
- b)50
- c)100
- d)125
- e)150
Correct answer is option 'E'. Can you explain this answer?
Most Upvoted Answer
Direction: Read the following data carefully and answer the questions ...
Given:
Total number of candidates appearing for the interview = 200
Number of candidates have scored more than 60% marks in their graduation = 50
Number of candidates scored more than 60% marks in both 12th standard and 10th standard = 90
Number of candidates scored more than 60% marks in 10th standard = 120
Number of candidates scored less than 60% marks at all the three stages – 10th standard, 12th standard, and graduation = 0
Concept Used:
Use of Venn diagrams.
Calculation:
The given conditions can be represented as Venn diagram as follows:
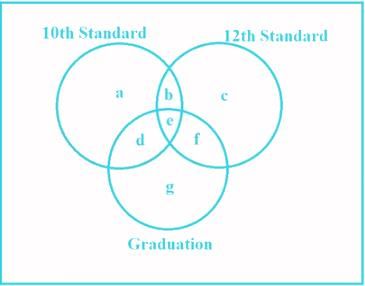
Here, a = Number of candidates scored more than 60% marks only in 10th standard,
b = Number of candidates scored more than 60% marks in both 10th standard and 12th standard,
c = Number of candidates scored more than 60% marks only in 12th standard,
d = Number of candidates scored more than 60% marks in both 10th standard and graduation,
e = Number of candidates scored more than 60% marks in 10th standard, 12th standard and graduation,
f = Number of candidates scored more than 60% marks in both 12th standard and graduation,
g = Number of candidates scored more than 60% marks only in graduation.
To obtain the sum of the total number of candidates, who got more than 60% marks in 10th standard only and those who got more than 60% marks in 12th standard only; we need to calculate the value of (a + c).
From the given conditions,
a + b + c + d + e + f + g = 200 ….(i)
d + e + f + g = 50 ….(ii)
On subtracting the values of equation (ii) from the value of equation (i), we get
a + b + c + d + e + f + g – (d + e + f + g) = 200 - 50
⇒ a + b + c = 150
∴ The total number of candidates, who were not able to score more than 60% in graduation; is 150
Confusion Point:
We need to take note of the fact that we are asked about "the total number of candidates who were not able to score more than 60% in graduation" and not "the total number of candidates who were not able to score more than 60% in graduation only". If the latter was asked, the answer would have simply been the value of (200 - g), and not the value of (a + b + c).
Total number of candidates appearing for the interview = 200
Number of candidates have scored more than 60% marks in their graduation = 50
Number of candidates scored more than 60% marks in both 12th standard and 10th standard = 90
Number of candidates scored more than 60% marks in 10th standard = 120
Number of candidates scored less than 60% marks at all the three stages – 10th standard, 12th standard, and graduation = 0
Concept Used:
Use of Venn diagrams.
Calculation:
The given conditions can be represented as Venn diagram as follows:

Here, a = Number of candidates scored more than 60% marks only in 10th standard,
b = Number of candidates scored more than 60% marks in both 10th standard and 12th standard,
c = Number of candidates scored more than 60% marks only in 12th standard,
d = Number of candidates scored more than 60% marks in both 10th standard and graduation,
e = Number of candidates scored more than 60% marks in 10th standard, 12th standard and graduation,
f = Number of candidates scored more than 60% marks in both 12th standard and graduation,
g = Number of candidates scored more than 60% marks only in graduation.
To obtain the sum of the total number of candidates, who got more than 60% marks in 10th standard only and those who got more than 60% marks in 12th standard only; we need to calculate the value of (a + c).
From the given conditions,
a + b + c + d + e + f + g = 200 ….(i)
d + e + f + g = 50 ….(ii)
On subtracting the values of equation (ii) from the value of equation (i), we get
a + b + c + d + e + f + g – (d + e + f + g) = 200 - 50
⇒ a + b + c = 150
∴ The total number of candidates, who were not able to score more than 60% in graduation; is 150
Confusion Point:
We need to take note of the fact that we are asked about "the total number of candidates who were not able to score more than 60% in graduation" and not "the total number of candidates who were not able to score more than 60% in graduation only". If the latter was asked, the answer would have simply been the value of (200 - g), and not the value of (a + b + c).
Free Test
FREE
| Start Free Test |
Community Answer
Direction: Read the following data carefully and answer the questions ...
Scored less than 60% marks in all three standards.
Question 1: How many candidates scored more than 60% marks in both graduation and 12th standard?
- From the given data, we know that 90 candidates scored more than 60% marks in both 12th standard and 10th standard. However, we do not have information about the number of candidates who scored more than 60% marks in both graduation and 12th standard. Therefore, we cannot determine the exact number of candidates who scored more than 60% marks in both graduation and 12th standard.
Question 2: How many candidates scored more than 60% marks in graduation but less than 60% marks in 12th standard?
- From the given data, we know that 50 candidates scored more than 60% marks in their graduation. However, we do not have information about the number of candidates who scored less than 60% marks in 12th standard. Therefore, we cannot determine the exact number of candidates who scored more than 60% marks in graduation but less than 60% marks in 12th standard.
Question 3: How many candidates scored more than 60% marks in 10th standard but less than 60% marks in graduation?
- From the given data, we know that 120 candidates scored more than 60% marks in 10th standard. However, we do not have information about the number of candidates who scored less than 60% marks in graduation. Therefore, we cannot determine the exact number of candidates who scored more than 60% marks in 10th standard but less than 60% marks in graduation.
Question 4: How many candidates scored more than 60% marks in all three standards?
- From the given data, we know that there was no candidate who scored less than 60% marks in all three standards. However, we do not have information about the number of candidates who scored more than 60% marks in all three standards. Therefore, we cannot determine the exact number of candidates who scored more than 60% marks in all three standards.
Question 1: How many candidates scored more than 60% marks in both graduation and 12th standard?
- From the given data, we know that 90 candidates scored more than 60% marks in both 12th standard and 10th standard. However, we do not have information about the number of candidates who scored more than 60% marks in both graduation and 12th standard. Therefore, we cannot determine the exact number of candidates who scored more than 60% marks in both graduation and 12th standard.
Question 2: How many candidates scored more than 60% marks in graduation but less than 60% marks in 12th standard?
- From the given data, we know that 50 candidates scored more than 60% marks in their graduation. However, we do not have information about the number of candidates who scored less than 60% marks in 12th standard. Therefore, we cannot determine the exact number of candidates who scored more than 60% marks in graduation but less than 60% marks in 12th standard.
Question 3: How many candidates scored more than 60% marks in 10th standard but less than 60% marks in graduation?
- From the given data, we know that 120 candidates scored more than 60% marks in 10th standard. However, we do not have information about the number of candidates who scored less than 60% marks in graduation. Therefore, we cannot determine the exact number of candidates who scored more than 60% marks in 10th standard but less than 60% marks in graduation.
Question 4: How many candidates scored more than 60% marks in all three standards?
- From the given data, we know that there was no candidate who scored less than 60% marks in all three standards. However, we do not have information about the number of candidates who scored more than 60% marks in all three standards. Therefore, we cannot determine the exact number of candidates who scored more than 60% marks in all three standards.

|
Explore Courses for Banking Exams exam
|

|
Question Description
Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer? for Banking Exams 2025 is part of Banking Exams preparation. The Question and answers have been prepared according to the Banking Exams exam syllabus. Information about Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer? covers all topics & solutions for Banking Exams 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer?.
Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer? for Banking Exams 2025 is part of Banking Exams preparation. The Question and answers have been prepared according to the Banking Exams exam syllabus. Information about Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer? covers all topics & solutions for Banking Exams 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer?.
Solutions for Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer? in English & in Hindi are available as part of our courses for Banking Exams.
Download more important topics, notes, lectures and mock test series for Banking Exams Exam by signing up for free.
Here you can find the meaning of Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer?, a detailed solution for Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer? has been provided alongside types of Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Direction: Read the following data carefully and answer the questions that follow: -A total of 200 candidates appear for an interview. A total of 50 candidates have scored more than 60% marks in their graduation. A total of 90 candidates scored more than 60% marks in both 12th standard and 10th standard. A total of 120 candidates scored more than 60% marks in 10th standard. Also, there was no candidate who couldn’t score more than 60% marks in atleast one of the stages – 10th standard, 12th standard, and graduation.Q.What is the total number of candidates, who were not able to score more than 60% in graduation?a)75b)50c)100d)125e)150Correct answer is option 'E'. Can you explain this answer? tests, examples and also practice Banking Exams tests.

|
Explore Courses for Banking Exams exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















