UGC NET Exam > UGC NET Questions > A walker travels along a one dimensional disc...
Start Learning for Free
A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given by
- a)0.5, 0.5
- b)0, 0.5
- c)0.25, 0
- d)0.25, 0.25
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
A walker travels along a one dimensional discrete lattice, labeled by ...
(i) 10 Steps:
- In this case, after 10 steps, the walker must take exactly 5 steps to the left (L) and 5 steps to the right (R), but the order in which these steps occur can vary.
- The total number of possible paths is 2^10 because each of the 10 steps can be either left or right, so there are 2 choices for each step. Now, we need to calculate the number of valid paths that return to the starting position. The number of ways to choose 5 out of 10 steps to be leftward (L) is given by the binomial coefficient :
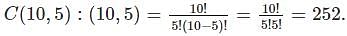
- Each of these combinations corresponds to a valid path that returns to the starting position. Therefore, there are 252 valid paths. Now, let's calculate the probability.
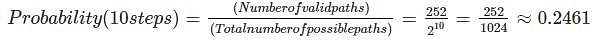
So, the correct probability for the walker to be at the same lattice position after 10 steps is approximately 0.2461, which can be rounded to 0.25.
(ii) 7 Steps:
- To find the probability that the walker is at the same lattice position after 7 steps, we need to consider the number of ways the walker can take steps to the left and right in such a way that the net displacement is zero. This is equivalent to counting the number of ways to arrange 3 steps to the left (L) and 4 steps to the right (R), or vice versa.
- The total number of arrangements is given by the binomial coefficient
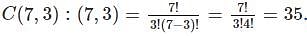
- However, for the walker to end up in the same position after 7 steps, there must be an equal number of steps to the left and right.
- Since 3 is not equal to 4, there are no valid arrangements that satisfy this condition. Therefore, the probability of the walker ending up at the same lattice position after 7 steps is indeed 0.
Free Test
FREE
| Start Free Test |
Community Answer
A walker travels along a one dimensional discrete lattice, labeled by ...
Probability of returning to the origin after certain steps
- After 10 steps:
- The walker has to take 5 steps to the left and 5 steps to the right to return to the origin.
- The number of ways this can happen is given by the binomial coefficient C(10,5).
- The total number of possible steps is 2^10 = 1024.
- Therefore, the probability of returning to the origin after 10 steps is C(10,5)/2^10 = 252/1024 = 0.25.
- After 7 steps:
- The walker has to take 3 steps to the left and 3 steps to the right to return to the origin.
- The number of ways this can happen is given by the binomial coefficient C(7,3).
- The total number of possible steps is 2^7 = 128.
- Therefore, the probability of returning to the origin after 7 steps is C(7,3)/2^7 = 35/128 ≈ 0.2734 ≈ 0.25.
Therefore, the correct answer is option 'C' with probabilities of 0.25 for both cases.
- After 10 steps:
- The walker has to take 5 steps to the left and 5 steps to the right to return to the origin.
- The number of ways this can happen is given by the binomial coefficient C(10,5).
- The total number of possible steps is 2^10 = 1024.
- Therefore, the probability of returning to the origin after 10 steps is C(10,5)/2^10 = 252/1024 = 0.25.
- After 7 steps:
- The walker has to take 3 steps to the left and 3 steps to the right to return to the origin.
- The number of ways this can happen is given by the binomial coefficient C(7,3).
- The total number of possible steps is 2^7 = 128.
- Therefore, the probability of returning to the origin after 7 steps is C(7,3)/2^7 = 35/128 ≈ 0.2734 ≈ 0.25.
Therefore, the correct answer is option 'C' with probabilities of 0.25 for both cases.
Attention UGC NET Students!
To make sure you are not studying endlessly, EduRev has designed UGC NET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in UGC NET.

|
Explore Courses for UGC NET exam
|

|
Similar UGC NET Doubts
A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer?
Question Description
A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer? for UGC NET 2024 is part of UGC NET preparation. The Question and answers have been prepared according to the UGC NET exam syllabus. Information about A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for UGC NET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer?.
A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer? for UGC NET 2024 is part of UGC NET preparation. The Question and answers have been prepared according to the UGC NET exam syllabus. Information about A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for UGC NET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer?.
Solutions for A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for UGC NET.
Download more important topics, notes, lectures and mock test series for UGC NET Exam by signing up for free.
Here you can find the meaning of A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A walker travels along a one dimensional discrete lattice, labeled by points –N, –N + 1, ...0, ..., N – 1, N, by putting random left and/or right steps of length l with equal probability for every step. Suppose the random walker starts from the lattice position 0 and is found at the same lattice position after (i) 10 and (ii) 7 step walks. The corresponding probabilities are respectively given bya)0.5, 0.5b)0, 0.5c)0.25, 0d)0.25, 0.25Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice UGC NET tests.

|
Explore Courses for UGC NET exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























