UGC NET Exam > UGC NET Questions > A silicon crystal is doped with phosphorus at...
Start Learning for Free
A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest to
- a)0.01 eV
- b)0.08 eV
- c)0.02 eV
- d)0.04 eV
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
A silicon crystal is doped with phosphorus atoms. (The binding energy ...
The energy levels of a donor atom in a silicon crystal are given by:

where ED is the energy of the donor level, me is the mass of an electron, m* is the effective mass of electrons in the crystal,
L is the length of the crystal, ℏℏ is the reduced Planck constant, and n is the quantum number.
The bottom of the conduction band in silicon occurs at the point where the energy is minimum, which is at the wave vector k = 0. The corresponding energy is:
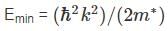
where m* is the effective mass of electrons in the crystal.
The gap between the donor energy level and the bottom of the conduction band is given by:
Egap = Emin - ED
Substituting the given values, we get:
m* = 0.4 me ED = -13.6 eV (since a phosphorus atom has one extra electron compared to silicon)
L = 1 nm (assuming a typical size for the crystal).
For the minimum energy in the conduction band, k = 0. Therefore:
Emin = 0.
Substituting these values into the expression for Egap, we get
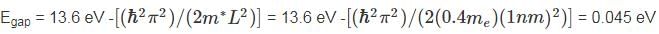
Therefore, the gap between the donor energy level and the bottom of the conduction band is nearest to 0.045 eV.

where ED is the energy of the donor level, me is the mass of an electron, m* is the effective mass of electrons in the crystal,
L is the length of the crystal, ℏℏ is the reduced Planck constant, and n is the quantum number.
The bottom of the conduction band in silicon occurs at the point where the energy is minimum, which is at the wave vector k = 0. The corresponding energy is:
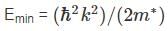
where m* is the effective mass of electrons in the crystal.
The gap between the donor energy level and the bottom of the conduction band is given by:
Egap = Emin - ED
Substituting the given values, we get:
m* = 0.4 me ED = -13.6 eV (since a phosphorus atom has one extra electron compared to silicon)
L = 1 nm (assuming a typical size for the crystal).
For the minimum energy in the conduction band, k = 0. Therefore:
Emin = 0.
Substituting these values into the expression for Egap, we get
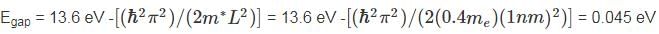
Therefore, the gap between the donor energy level and the bottom of the conduction band is nearest to 0.045 eV.
Most Upvoted Answer
A silicon crystal is doped with phosphorus atoms. (The binding energy ...
Let's break down the problem step by step to understand why the correct answer is option 'D'.
1. Understanding Doping:
Doping is the process of intentionally introducing impurities into a semiconductor crystal to modify its electrical properties. In this case, the silicon crystal is doped with phosphorus atoms.
2. Donor Energy Level:
When phosphorus atoms are introduced into the silicon crystal, they act as donors, providing excess electrons to the crystal. These excess electrons occupy energy levels just below the conduction band and are called donor energy levels.
3. Energy Gap:
The energy gap is the difference in energy between the valence band (where electrons are normally bound to atoms) and the conduction band (where electrons are free to move and conduct electricity). In an undoped silicon crystal, this energy gap is typically around 1.1 eV.
4. Effective Mass of Electrons:
The effective mass of electrons in a crystal is the mass they appear to have when moving within the crystal lattice. In this case, the effective mass of electrons in the silicon crystal is given as 0.4 me, where me is the rest mass of an electron.
5. Binding Energy of Hydrogen Atom:
The binding energy of a hydrogen atom is the amount of energy required to remove an electron from the hydrogen atom and make it free. In this case, the binding energy of a hydrogen atom is given as 13.6 eV.
6. Dielectric Constant of Silicon:
The dielectric constant of silicon is a measure of how much the electric field within the crystal is reduced compared to the electric field in vacuum. In this case, the dielectric constant of silicon is given as 12.
7. Analysis:
The gap between the donor energy level and the bottom of the conduction band can be calculated using the equation:
ΔE = E_don - E_con
where ΔE is the energy gap, E_don is the donor energy level, and E_con is the bottom of the conduction band.
We know that the binding energy of a hydrogen atom is equal to the energy required to remove an electron from the donor energy level. Therefore, the energy of the donor energy level can be written as:
E_don = 13.6 eV
The energy of the bottom of the conduction band can be calculated using the equation:
E_con = E_val + Eg
where E_val is the energy of the valence band and Eg is the energy gap.
The energy of the valence band can be written as:
E_val = -13.6 eV (since it is the negative of the binding energy of a hydrogen atom)
Substituting the given values, we have:
E_con = -13.6 eV + 1.1 eV = -12.5 eV
Finally, we can calculate the energy gap:
ΔE = E_don - E_con = 13.6 eV - (-12.5 eV) = 26.1 eV
8. Answer:
The gap between the donor energy level and the bottom of the conduction band is approximately 26.1 eV. Among the given options, the nearest value to 26.1 eV is option 'D' (0.04 eV).
Therefore, the correct answer is option 'D' (0.04 eV).
1. Understanding Doping:
Doping is the process of intentionally introducing impurities into a semiconductor crystal to modify its electrical properties. In this case, the silicon crystal is doped with phosphorus atoms.
2. Donor Energy Level:
When phosphorus atoms are introduced into the silicon crystal, they act as donors, providing excess electrons to the crystal. These excess electrons occupy energy levels just below the conduction band and are called donor energy levels.
3. Energy Gap:
The energy gap is the difference in energy between the valence band (where electrons are normally bound to atoms) and the conduction band (where electrons are free to move and conduct electricity). In an undoped silicon crystal, this energy gap is typically around 1.1 eV.
4. Effective Mass of Electrons:
The effective mass of electrons in a crystal is the mass they appear to have when moving within the crystal lattice. In this case, the effective mass of electrons in the silicon crystal is given as 0.4 me, where me is the rest mass of an electron.
5. Binding Energy of Hydrogen Atom:
The binding energy of a hydrogen atom is the amount of energy required to remove an electron from the hydrogen atom and make it free. In this case, the binding energy of a hydrogen atom is given as 13.6 eV.
6. Dielectric Constant of Silicon:
The dielectric constant of silicon is a measure of how much the electric field within the crystal is reduced compared to the electric field in vacuum. In this case, the dielectric constant of silicon is given as 12.
7. Analysis:
The gap between the donor energy level and the bottom of the conduction band can be calculated using the equation:
ΔE = E_don - E_con
where ΔE is the energy gap, E_don is the donor energy level, and E_con is the bottom of the conduction band.
We know that the binding energy of a hydrogen atom is equal to the energy required to remove an electron from the donor energy level. Therefore, the energy of the donor energy level can be written as:
E_don = 13.6 eV
The energy of the bottom of the conduction band can be calculated using the equation:
E_con = E_val + Eg
where E_val is the energy of the valence band and Eg is the energy gap.
The energy of the valence band can be written as:
E_val = -13.6 eV (since it is the negative of the binding energy of a hydrogen atom)
Substituting the given values, we have:
E_con = -13.6 eV + 1.1 eV = -12.5 eV
Finally, we can calculate the energy gap:
ΔE = E_don - E_con = 13.6 eV - (-12.5 eV) = 26.1 eV
8. Answer:
The gap between the donor energy level and the bottom of the conduction band is approximately 26.1 eV. Among the given options, the nearest value to 26.1 eV is option 'D' (0.04 eV).
Therefore, the correct answer is option 'D' (0.04 eV).

|
Explore Courses for UGC NET exam
|

|
Similar UGC NET Doubts
A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer?
Question Description
A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer? for UGC NET 2025 is part of UGC NET preparation. The Question and answers have been prepared according to the UGC NET exam syllabus. Information about A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for UGC NET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer?.
A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer? for UGC NET 2025 is part of UGC NET preparation. The Question and answers have been prepared according to the UGC NET exam syllabus. Information about A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for UGC NET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer?.
Solutions for A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for UGC NET.
Download more important topics, notes, lectures and mock test series for UGC NET Exam by signing up for free.
Here you can find the meaning of A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A silicon crystal is doped with phosphorus atoms. (The binding energy of a H atom is 13.6 eV, the dielectric constant of silicon is 12 and the effective mass of electrons in the crystal is 0.4 me) The gap between the donor energy level and the bottom of the conduction band is nearest toa)0.01 eVb)0.08 eVc)0.02 eVd)0.04 eVCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice UGC NET tests.

|
Explore Courses for UGC NET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























