Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > Vertical columns of the same material, height...
Start Learning for Free
Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?
- a)Solid circular section
- b)Thin hollow circular section
- c)I - section
- d)Solid square section
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
Vertical columns of the same material, height and weight have the same...
Concept: Columns can be classified as :
- Long columns: Fails due to buckling.
- Short columns: Fails due to crushing.
- Intermediate columns: Fails due to both crushing and buckling.
For a long column Euler's load is given by,
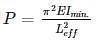
where, E = modulus of elasticity, Imin. = Minor principal moment of inertia, Leff = Effective length (depends on the end conditions of the column)
So,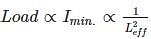
For same end conditions:
Effective length (Leff) will remain same for every cross section of the column.
Thus, Load ∝ Imin.
Hence the maximum load will be carried by the column having largest value of minor principal moment of inertia.
In the given four shapes Moment of inertia is maximum for thin hollow circular section because the maximum mass in this case, lies away from the centroidal axis as compared to all other cross sections. Hence the load carrying capacity is maximum for the thin hollow circular section.
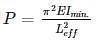
where, E = modulus of elasticity, Imin. = Minor principal moment of inertia, Leff = Effective length (depends on the end conditions of the column)
So,
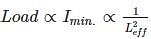
For same end conditions:
Effective length (Leff) will remain same for every cross section of the column.
Thus, Load ∝ Imin.
Hence the maximum load will be carried by the column having largest value of minor principal moment of inertia.
In the given four shapes Moment of inertia is maximum for thin hollow circular section because the maximum mass in this case, lies away from the centroidal axis as compared to all other cross sections. Hence the load carrying capacity is maximum for the thin hollow circular section.
Most Upvoted Answer
Vertical columns of the same material, height and weight have the same...
Introduction:
In this question, we are given that vertical columns of the same material, height, and weight have the same end conditions. We need to determine which cross-section will carry the maximum load.
Analysis:
To determine the cross-section that can carry the maximum load, we need to consider the strength and stiffness of different cross-sections. The load-carrying capacity of a column is influenced by its moment of inertia, which is a measure of its resistance to bending.
Options:
Let's analyze each option one by one:
a) Solid circular section:
- The solid circular section has a symmetrical shape, which provides uniform resistance to bending.
- It has a higher moment of inertia compared to other sections.
- Due to its symmetrical shape, it can efficiently distribute the load along its circumference.
- Therefore, the solid circular section is a good choice for load-carrying capacity.
b) Thin hollow circular section:
- The thin hollow circular section consists of an outer and inner circular shape.
- It has a larger moment of inertia compared to other sections, including the solid circular section.
- The distribution of material in the hollow section adds extra stiffness and strength.
- Due to its larger moment of inertia and added stiffness, the thin hollow circular section can carry a higher load compared to other sections.
- Therefore, the thin hollow circular section is the correct answer for maximum load-carrying capacity.
c) I-section:
- The I-section consists of a vertical web and horizontal flanges.
- It provides high strength and stiffness, especially in the vertical direction.
- However, the moment of inertia of the I-section is usually smaller compared to the circular sections.
- Therefore, the I-section may not be able to carry as much load as the circular sections.
d) Solid square section:
- The solid square section has a symmetrical shape, but it has a smaller moment of inertia compared to circular sections.
- The distribution of material in the square section is not as efficient as in the circular sections.
- Therefore, the solid square section may not be able to carry as much load as the circular sections.
Conclusion:
Among the given options, the thin hollow circular section is the cross-section that can carry the maximum load. It has a larger moment of inertia and added stiffness due to the distribution of material in the hollow section.
In this question, we are given that vertical columns of the same material, height, and weight have the same end conditions. We need to determine which cross-section will carry the maximum load.
Analysis:
To determine the cross-section that can carry the maximum load, we need to consider the strength and stiffness of different cross-sections. The load-carrying capacity of a column is influenced by its moment of inertia, which is a measure of its resistance to bending.
Options:
Let's analyze each option one by one:
a) Solid circular section:
- The solid circular section has a symmetrical shape, which provides uniform resistance to bending.
- It has a higher moment of inertia compared to other sections.
- Due to its symmetrical shape, it can efficiently distribute the load along its circumference.
- Therefore, the solid circular section is a good choice for load-carrying capacity.
b) Thin hollow circular section:
- The thin hollow circular section consists of an outer and inner circular shape.
- It has a larger moment of inertia compared to other sections, including the solid circular section.
- The distribution of material in the hollow section adds extra stiffness and strength.
- Due to its larger moment of inertia and added stiffness, the thin hollow circular section can carry a higher load compared to other sections.
- Therefore, the thin hollow circular section is the correct answer for maximum load-carrying capacity.
c) I-section:
- The I-section consists of a vertical web and horizontal flanges.
- It provides high strength and stiffness, especially in the vertical direction.
- However, the moment of inertia of the I-section is usually smaller compared to the circular sections.
- Therefore, the I-section may not be able to carry as much load as the circular sections.
d) Solid square section:
- The solid square section has a symmetrical shape, but it has a smaller moment of inertia compared to circular sections.
- The distribution of material in the square section is not as efficient as in the circular sections.
- Therefore, the solid square section may not be able to carry as much load as the circular sections.
Conclusion:
Among the given options, the thin hollow circular section is the cross-section that can carry the maximum load. It has a larger moment of inertia and added stiffness due to the distribution of material in the hollow section.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer?
Question Description
Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer?.
Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer?.
Solutions for Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Vertical columns of the same material, height and weight have the same end conditions. Which cross-section will carry the maximum load?a)Solid circular sectionb)Thin hollow circular sectionc)I - sectiond)Solid square sectionCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























