JEE Exam > JEE Questions > A monochromatic light is incident on a hydrog...
Start Learning for Free
A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x × 1015 Hz. The value of x is ____________.
(Given h = 4.25 × 10-15 eVs)
Correct answer is '3'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
A monochromatic light is incident on a hydrogen sample in ground state...
When a monochromatic light is incident on hydrogen atoms in the ground state (n = 1), the hydrogen atoms can absorb energy and transition to higher energy levels. When the atoms return to lower energy levels, they emit radiation of different wavelengths corresponding to the energy differences between the energy levels.
The energy levels of the hydrogen atom are given by the formula:
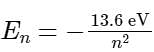
where En is the energy of the nth level and n is the principal quantum number.
Since the hydrogen atoms emit radiation of six different wavelengths, there must be six different transitions from the excited states back to lower energy levels.
The six transitions correspond to the following energy level changes:
From n = 2 to n = 1
From n = 3 to n = 1
From n = 3 to n = 2
From n = 4 to n = 1
From n = 4 to n = 2
From n = 4 to n = 3
From n = 3 to n = 1
From n = 3 to n = 2
From n = 4 to n = 1
From n = 4 to n = 2
From n = 4 to n = 3
The highest energy level involved is n = 4. Therefore, the incident light must have a frequency high enough to excite the hydrogen atoms from the ground state (n = 1) to n = 4.
The energy difference between these levels is:
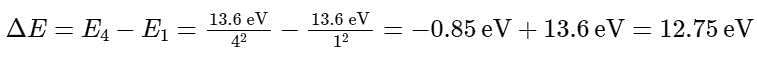
The frequency of the incident light is related to the energy difference by the equation:
ΔE = hv
where h is the Planck's constant and v is the frequency.
Now, we can solve for the frequency:
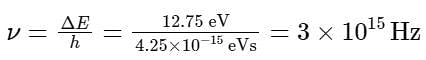
So, the value of x is 3.
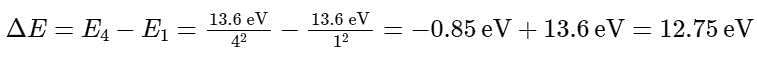
The frequency of the incident light is related to the energy difference by the equation:
ΔE = hv
where h is the Planck's constant and v is the frequency.
Now, we can solve for the frequency:
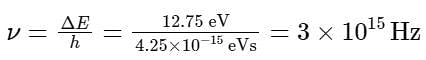
So, the value of x is 3.
Free Test
FREE
| Start Free Test |
Community Answer
A monochromatic light is incident on a hydrogen sample in ground state...
Let us consider the absorption and emission processes of the hydrogen atoms.
When the monochromatic light is incident on the hydrogen sample, some of the hydrogen atoms will absorb the light. This absorption causes the electrons in the hydrogen atoms to transition from lower energy levels to higher energy levels.
Since the hydrogen sample is in the ground state initially, the absorbed light must have energy equal to the energy difference between the ground state and the excited states. The energy difference between the ground state and the excited states in the hydrogen atom is given by the Rydberg formula:
E = -13.6 eV / n²
where E is the energy in electron volts (eV) and n is the principal quantum number representing the energy level.
Now, let's consider the emission process. After absorbing the light and being in the excited state, the hydrogen atoms will spontaneously transition back to lower energy levels, releasing energy in the form of light. The emitted light will have frequencies corresponding to the energy differences between the excited states and the ground state.
The frequency of light is given by the equation:
ν = ΔE / h
where ν is the frequency, ΔE is the energy difference, and h is Planck's constant.
Since the hydrogen atoms emit radiation of six different wavelengths, this means that the absorbed light must have had energy differences corresponding to these six possible transitions. Let's represent these energy differences as ΔE₁, ΔE₂, ΔE₃, ΔE₄, ΔE₅, and ΔE₆.
Therefore, we have the following equations:
ΔE₁ = -13.6 eV / n₁²
ΔE₂ = -13.6 eV / n₂²
ΔE₃ = -13.6 eV / n₃²
ΔE₄ = -13.6 eV / n₄²
ΔE₅ = -13.6 eV / n₅²
ΔE₆ = -13.6 eV / n₆²
where n₁, n₂, n₃, n₄, n₅, and n₆ are the principal quantum numbers corresponding to the energy levels of the excited states.
Since the absorbed light has a frequency x, we can equate it to one of the energy differences:
x = ΔE₁ / h
Solving this equation for n₁², we get:
n₁² = -13.6 eV / (x * h)
Similarly, we can equate the frequencies of the emitted light to the corresponding energy differences:
ν₁ = ΔE₁ / h = -13.6 eV / (n₁² * h)
ν₂ = ΔE₂ / h = -13.6 eV / (n₂² * h)
ν₃ = ΔE₃ / h = -13.6 eV / (n₃² * h)
ν₄ = ΔE₄ / h = -13.6 eV / (n₄² * h)
ν₅ = ΔE₅ / h = -13.6 eV / (n₅² * h)
ν₆ = ΔE₆ / h = -13.6 eV / (n₆² * h)
Using the equation for n₁² derived earlier, we can express the frequencies
When the monochromatic light is incident on the hydrogen sample, some of the hydrogen atoms will absorb the light. This absorption causes the electrons in the hydrogen atoms to transition from lower energy levels to higher energy levels.
Since the hydrogen sample is in the ground state initially, the absorbed light must have energy equal to the energy difference between the ground state and the excited states. The energy difference between the ground state and the excited states in the hydrogen atom is given by the Rydberg formula:
E = -13.6 eV / n²
where E is the energy in electron volts (eV) and n is the principal quantum number representing the energy level.
Now, let's consider the emission process. After absorbing the light and being in the excited state, the hydrogen atoms will spontaneously transition back to lower energy levels, releasing energy in the form of light. The emitted light will have frequencies corresponding to the energy differences between the excited states and the ground state.
The frequency of light is given by the equation:
ν = ΔE / h
where ν is the frequency, ΔE is the energy difference, and h is Planck's constant.
Since the hydrogen atoms emit radiation of six different wavelengths, this means that the absorbed light must have had energy differences corresponding to these six possible transitions. Let's represent these energy differences as ΔE₁, ΔE₂, ΔE₃, ΔE₄, ΔE₅, and ΔE₆.
Therefore, we have the following equations:
ΔE₁ = -13.6 eV / n₁²
ΔE₂ = -13.6 eV / n₂²
ΔE₃ = -13.6 eV / n₃²
ΔE₄ = -13.6 eV / n₄²
ΔE₅ = -13.6 eV / n₅²
ΔE₆ = -13.6 eV / n₆²
where n₁, n₂, n₃, n₄, n₅, and n₆ are the principal quantum numbers corresponding to the energy levels of the excited states.
Since the absorbed light has a frequency x, we can equate it to one of the energy differences:
x = ΔE₁ / h
Solving this equation for n₁², we get:
n₁² = -13.6 eV / (x * h)
Similarly, we can equate the frequencies of the emitted light to the corresponding energy differences:
ν₁ = ΔE₁ / h = -13.6 eV / (n₁² * h)
ν₂ = ΔE₂ / h = -13.6 eV / (n₂² * h)
ν₃ = ΔE₃ / h = -13.6 eV / (n₃² * h)
ν₄ = ΔE₄ / h = -13.6 eV / (n₄² * h)
ν₅ = ΔE₅ / h = -13.6 eV / (n₅² * h)
ν₆ = ΔE₆ / h = -13.6 eV / (n₆² * h)
Using the equation for n₁² derived earlier, we can express the frequencies
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.

|
Explore Courses for JEE exam
|

|
Similar JEE Doubts
A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer?
Question Description
A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer?.
A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer?.
Solutions for A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer?, a detailed solution for A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer? has been provided alongside types of A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is x× 1015 Hz.The value of x is ____________.(Given h = 4.25×10-15eVs)Correct answer is '3'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























