CAT Exam > CAT Questions > A mixture P is formed by removing a certain a...
Start Learning for Free
A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q is
- a)4 : 9
- b)1 : 3
- c)5 : 9
- d)1 : 2
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A mixture P is formed by removing a certain amount of coffee from a co...
Every time 20% of the mixture is replace with a pure adulterant (here cocoa), the concentration of the mixture becomes 80% of the initial concentration.
Similarly when a proportion p of a mixture is replaced with pure adulterant, the concentration of the mixture becomes (1 - p) times the previous concentration. (0 ≤ p ≤ 1)
Initially there was pure coffee, so the strength of the mixture is 100% or 1 (in terms of proportion)
Let a proportion p of the mixture be replaced each time… Since after repeating the process twice, we have the concentration of coffee as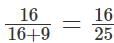
at the end of the two replacements.
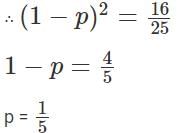
Or, 20% of the mixture is replaced each time.
The ratio of cocoa powder in the mixture P and Q will then be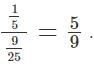
Similarly when a proportion p of a mixture is replaced with pure adulterant, the concentration of the mixture becomes (1 - p) times the previous concentration. (0 ≤ p ≤ 1)
Initially there was pure coffee, so the strength of the mixture is 100% or 1 (in terms of proportion)
Let a proportion p of the mixture be replaced each time… Since after repeating the process twice, we have the concentration of coffee as
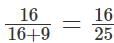at the end of the two replacements.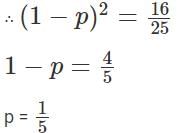Or, 20% of the mixture is replaced each time.
The ratio of cocoa powder in the mixture P and Q will then be
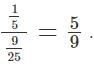
Most Upvoted Answer
A mixture P is formed by removing a certain amount of coffee from a co...
Understanding the Problem:
The problem involves two mixtures, P and Q, which are obtained by a process of replacing coffee with cocoa powder. We need to find the ratio of cocoa in mixture P to that in mixture Q.
Solution:
- Let the initial amount of coffee in the jar be C and the initial amount of cocoa be K.
- In mixture P, when the same amount of coffee is removed and replaced by cocoa powder, the ratio of coffee to cocoa remains the same as in the original mixture. Therefore, the ratio of coffee to cocoa in mixture P is C:K.
- In mixture Q, after the second replacement, the ratio of coffee to cocoa is given as 16:9.
- Since the amount of coffee and cocoa removed and added is the same in both P and Q, the ratio of coffee to cocoa in mixture Q is also C:K.
- From the given ratio 16:9, we can write C/K = 16/9.
- Now, we need to find the ratio of cocoa in mixture P to that in mixture Q, which would be K (cocoa in mixture P) / K (cocoa in mixture Q) = 9/16.
- Therefore, the ratio of cocoa in mixture P to that in mixture Q is 9:16, which is equivalent to 5:9.
Therefore, the correct answer is option C) 5:9.
The problem involves two mixtures, P and Q, which are obtained by a process of replacing coffee with cocoa powder. We need to find the ratio of cocoa in mixture P to that in mixture Q.
Solution:
- Let the initial amount of coffee in the jar be C and the initial amount of cocoa be K.
- In mixture P, when the same amount of coffee is removed and replaced by cocoa powder, the ratio of coffee to cocoa remains the same as in the original mixture. Therefore, the ratio of coffee to cocoa in mixture P is C:K.
- In mixture Q, after the second replacement, the ratio of coffee to cocoa is given as 16:9.
- Since the amount of coffee and cocoa removed and added is the same in both P and Q, the ratio of coffee to cocoa in mixture Q is also C:K.
- From the given ratio 16:9, we can write C/K = 16/9.
- Now, we need to find the ratio of cocoa in mixture P to that in mixture Q, which would be K (cocoa in mixture P) / K (cocoa in mixture Q) = 9/16.
- Therefore, the ratio of cocoa in mixture P to that in mixture Q is 9:16, which is equivalent to 5:9.
Therefore, the correct answer is option C) 5:9.
|
Explore Courses for CAT exam
|
|
Similar CAT Doubts
Top Courses for CATView all
A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer?
Question Description
A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer?.
A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer?.
Solutions for A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q isa)4 : 9b)1 : 3c)5 : 9d)1 : 2Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice CAT tests.
|
|
Explore Courses for CAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup