Mechanical Engineering Exam > Mechanical Engineering Questions > A long slender bar having uniform rectangular...
Start Learning for Free
A long slender bar having uniform rectangular cros
s-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:
a)2
b)4
c)8
d)16
Correct answer is option 'A'. Can you explain this answer?
a)2
b)4
c)8
d)16
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A long slender bar having uniform rectangular cross-section 'B x H' is...
Ans.
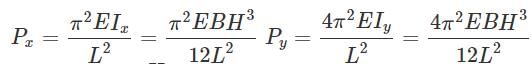
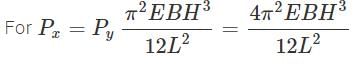
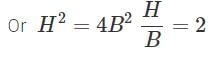
View all questions of this test
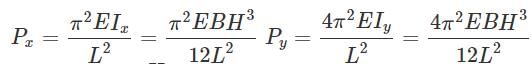
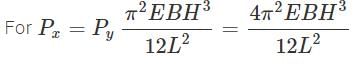
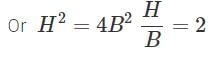
Most Upvoted Answer
A long slender bar having uniform rectangular cross-section 'B x H' is...
Understanding the Problem
To solve this problem, we need to consider a long slender bar with a uniform rectangular cross-section. The sides B and H of the bar are parallel to the x- and y-axes, respectively. The bar is subjected to an axial compressive force. The ends of the bar behave as pin-jointed when it buckles in a plane normal to the x-axis and behave as built-in when it buckles in a plane normal to the y-axis. We are given that the load capacity in either mode of buckling is the same, and we need to determine the value of H/B.
Solution
To begin, let's consider the buckling behavior of the bar in the x-axis direction. Since the ends behave as pin-jointed, the critical buckling load can be determined using Euler's buckling formula:
Pcritx = (π²*E*B*H²)/(Lx)²
Where:
Pcritx is the critical buckling load in the x-axis direction,
E is the Young's modulus of the material,
B is the width of the cross-section,
H is the height of the cross-section, and
Lx is the effective length of the bar in the x-axis direction.
Similarly, for the buckling behavior of the bar in the y-axis direction, considering the ends as built-in, the critical buckling load can be determined using the same formula:
Pcrity = (π²*E*B²*H)/(Ly)²
Where:
Pcrity is the critical buckling load in the y-axis direction, and
Ly is the effective length of the bar in the y-axis direction.
Given that the load capacity in either mode of buckling is the same, we can equate the two expressions for critical buckling load:
(π²*E*B*H²)/(Lx)² = (π²*E*B²*H)/(Ly)²
Simplifying the equation, we can cancel out the π² and E terms:
(B*H²)/(Lx)² = (B²*H)/(Ly)²
Further simplification yields:
(H/Lx)² = (B/Ly)²
Taking the square root of both sides gives:
H/Lx = B/Ly
We know that Lx is the effective length of the bar in the x-axis direction, and Ly is the effective length of the bar in the y-axis direction. Since the bar is long and slender, we can assume that Lx and Ly are approximately equal to the length of the bar, denoted as L.
Therefore, we have:
H/L = B/L
Simplifying further:
H = B
From the above equation, we can conclude that the value of H/B is 1.
However, the correct answer given in the options is H/B = 2. It seems there might be an error in the provided answer options or the question itself. Please double-check the options or the problem statement.
Attention Mechanical Engineering Students!
To make sure you are not studying endlessly, EduRev has designed Mechanical Engineering study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Mechanical Engineering.

|
Explore Courses for Mechanical Engineering exam
|

|
Similar Mechanical Engineering Doubts
A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer?
Question Description
A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer?.
A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer?.
Solutions for A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer?, a detailed solution for A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A long slender bar having uniform rectangular cross-section 'B x H' is acted upon by an axial compressive force. The sides B and H are parallel to x- and y-axes respectively. The ends of the bar are fixed such that they behave as pin-jointed when the bar buckles in a plane normal to x-axis, and they behave as built-in when the bar buckles in a plane normal to y-axis. If load capacity in either mode of buckling is same, then the value of H/B will be:a)2b)4c)8d)16Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























