Class 12 Exam > Class 12 Questions > A mineral having the formula AB2 crystallises...
Start Learning for Free
A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms is
- a)0.52
- b)0.68
- c)0.74
- d)1.00
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A mineral having the formula AB2 crystallises in the cubic closest - p...
A CN=8 Cubic coordination
B CN=4 Tetrahedral coordination
AB2 type crystal structure (CaF2):
Blue – Ca
Yellow- F
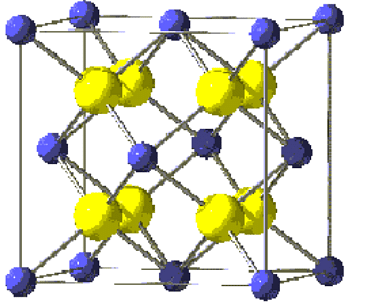
Co ordination number of A(For example Ca)= 8 (White one is surrounded by 8 neighbours)
Co ordination number of B(For example F)= 4 (yellow one is surrounded by 4 neighbours)
Most Upvoted Answer
A mineral having the formula AB2 crystallises in the cubic closest - p...
Solution:
Given: A mineral having formula AB2 crystallizes in cubic closest - packed lattice with A-atoms occupying the lattice points.
To find: Fraction of tetrahedral sites occupied by 6-atoms
Explanation:
- In cubic closest-packed lattice, there are 4 tetrahedral voids and 8 octahedral voids per unit cell.
- Since the formula of the mineral is AB2, there are 2 B-atoms for every A-atom. Therefore, the number of tetrahedral sites occupied by B-atoms = 2 x number of A-atoms.
- Let the number of A-atoms in the unit cell be x. Then, the number of B-atoms in the unit cell is 2x.
- Since the A-atoms occupy the lattice points, they do not occupy any of the tetrahedral or octahedral voids.
- Let the fraction of tetrahedral sites occupied by B-atoms be y.
- Then, the number of B-atoms occupying tetrahedral sites = y x 4x = 4y x^2
- Since each tetrahedral site is surrounded by 4 atoms, the total number of atoms surrounding the tetrahedral sites = 4 x 4 = 16.
- Therefore, the number of 6-atom molecules surrounding the tetrahedral sites = (16/6) x (4y x^2) = 32/3 y x^2
- Since the total number of atoms in the unit cell = x + 2x = 3x, the fraction of tetrahedral sites occupied by 6-atoms = (32/3 y x^2)/(6x) = 16/9 y
To find the value of y, we need to use the fact that the mineral crystallizes in cubic closest-packed lattice.
- In cubic closest-packed lattice, each sphere is surrounded by 12 nearest neighbors arranged in the form of an octahedron.
- Therefore, the number of octahedral voids = number of spheres.
- Let the radius of the A-atom be rA and the radius of the B-atom be rB.
- Since the A-atoms occupy the lattice points, the distance between two adjacent A-atoms = 2rA.
- The radius of the octahedral void = rO = (sqrt(2)/2) x 2rA = sqrt(2) x rA
- The distance between the centers of two adjacent octahedral voids = 4rO = 4 x sqrt(2) x rA.
- Therefore, the length of the edge of the unit cell = 4 x sqrt(2) x rA.
- The distance between the center of an octahedral void and the center of the closest A-atom = rA + rO = (1 + sqrt(2)) x rA.
- Therefore, the distance between the centers of two adjacent tetrahedral voids = 2 x (1 + sqrt(2)) x rA.
- Let the distance between two adjacent B-atoms occupying the tetrahedral voids be d.
- Then, d^2 = (2 x (1 + sqrt(2)) x rA)^2 + (2rB)^2
- Since the mineral crystallizes in cubic closest-packed lattice, the distance between two adjacent B
Given: A mineral having formula AB2 crystallizes in cubic closest - packed lattice with A-atoms occupying the lattice points.
To find: Fraction of tetrahedral sites occupied by 6-atoms
Explanation:
- In cubic closest-packed lattice, there are 4 tetrahedral voids and 8 octahedral voids per unit cell.
- Since the formula of the mineral is AB2, there are 2 B-atoms for every A-atom. Therefore, the number of tetrahedral sites occupied by B-atoms = 2 x number of A-atoms.
- Let the number of A-atoms in the unit cell be x. Then, the number of B-atoms in the unit cell is 2x.
- Since the A-atoms occupy the lattice points, they do not occupy any of the tetrahedral or octahedral voids.
- Let the fraction of tetrahedral sites occupied by B-atoms be y.
- Then, the number of B-atoms occupying tetrahedral sites = y x 4x = 4y x^2
- Since each tetrahedral site is surrounded by 4 atoms, the total number of atoms surrounding the tetrahedral sites = 4 x 4 = 16.
- Therefore, the number of 6-atom molecules surrounding the tetrahedral sites = (16/6) x (4y x^2) = 32/3 y x^2
- Since the total number of atoms in the unit cell = x + 2x = 3x, the fraction of tetrahedral sites occupied by 6-atoms = (32/3 y x^2)/(6x) = 16/9 y
To find the value of y, we need to use the fact that the mineral crystallizes in cubic closest-packed lattice.
- In cubic closest-packed lattice, each sphere is surrounded by 12 nearest neighbors arranged in the form of an octahedron.
- Therefore, the number of octahedral voids = number of spheres.
- Let the radius of the A-atom be rA and the radius of the B-atom be rB.
- Since the A-atoms occupy the lattice points, the distance between two adjacent A-atoms = 2rA.
- The radius of the octahedral void = rO = (sqrt(2)/2) x 2rA = sqrt(2) x rA
- The distance between the centers of two adjacent octahedral voids = 4rO = 4 x sqrt(2) x rA.
- Therefore, the length of the edge of the unit cell = 4 x sqrt(2) x rA.
- The distance between the center of an octahedral void and the center of the closest A-atom = rA + rO = (1 + sqrt(2)) x rA.
- Therefore, the distance between the centers of two adjacent tetrahedral voids = 2 x (1 + sqrt(2)) x rA.
- Let the distance between two adjacent B-atoms occupying the tetrahedral voids be d.
- Then, d^2 = (2 x (1 + sqrt(2)) x rA)^2 + (2rB)^2
- Since the mineral crystallizes in cubic closest-packed lattice, the distance between two adjacent B
Free Test
FREE
| Start Free Test |
Community Answer
A mineral having the formula AB2 crystallises in the cubic closest - p...
(d) AB2 crystallises as cubic close packed (ccp).
Thus, A2+ is surrounded by eight B- and B- is surrounded by four A2+ .
Thus, coordinatio n number of A2+ = B
coordination number of B- = 4
Number of atoms in tetrahedral in small cube of unit cell of atom B = 4
Thus, fraction occupied = 4/4 = 1 (100%)
Thus, A2+ is surrounded by eight B- and B- is surrounded by four A2+ .
Thus, coordinatio n number of A2+ = B
coordination number of B- = 4
Number of atoms in tetrahedral in small cube of unit cell of atom B = 4
Thus, fraction occupied = 4/4 = 1 (100%)

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer?
Question Description
A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer?.
A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer?.
Solutions for A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer?, a detailed solution for A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A mineral having the formula AB2 crystallises in the cubic closest - packed lattice with the A-atoms occupying the lattice points. Fraction of the tetrahedral sites occupied by 6-atoms isa)0.52b)0.68c)0.74d)1.00Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















