Mechanical Engineering Exam > Mechanical Engineering Questions > A sprue for avoiding aspiration todeliver liq...
Start Learning for Free
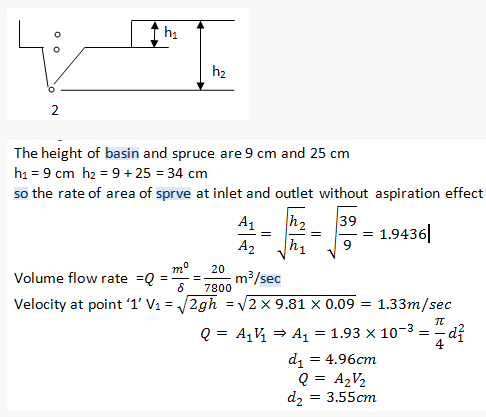
A sprue for avoiding aspiration to deliver liquid iron at a rate of 20 kg/s. The density of iron is 7800 kg/m3. The height of pouring basin is 9cm. and height of sprue is 25cm. Diameter of sprue base is:-
- a)3.55 cm
- b)4.55 cm
- c)3.75 cm
- d)5.75 cm
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A sprue for avoiding aspiration todeliver liquid iron at a rate of 20k...
Most Upvoted Answer
A sprue for avoiding aspiration todeliver liquid iron at a rate of 20k...
Calculation of Diameter of Sprue Base
Given:
Rate of delivery of liquid iron = 20 kg/s
Density of iron = 7800 kg/m3
Height of pouring basin = 9 cm
Height of sprue = 25 cm
Let's calculate the pressure head of liquid iron in the sprue using Bernoulli's equation:
P1/ρg + v1^2/2g + h1 = P2/ρg + v2^2/2g + h2
where,
P1 = pressure at the surface of the liquid iron in the pouring basin (atmospheric pressure)
P2 = pressure at the base of the sprue (unknown)
ρ = density of liquid iron
g = acceleration due to gravity
v1 = velocity of liquid iron at the surface of the pouring basin (zero)
v2 = velocity of liquid iron at the base of the sprue (unknown)
h1 = height of the surface of the liquid iron above the base of the sprue (9 cm + 25 cm = 34 cm)
h2 = height of the base of the sprue above the surface of the liquid iron in the pouring basin (unknown)
Substituting the given values, we get:
P2/7800g + v2^2/2g + 0.34 m = Patm/7800g + 0
where Patm is atmospheric pressure.
Since the velocity of liquid iron at the base of the sprue is negligible compared to the velocity at the surface of the pouring basin, we can neglect the second term.
Solving for P2, we get:
P2 = (Patm + 7800g x 0.34) Pa
Next, we can calculate the velocity of liquid iron at the base of the sprue using the equation of continuity:
A1v1 = A2v2
where A1 and A2 are the cross-sectional areas of the pouring basin and sprue, respectively.
Assuming the pouring basin has a larger diameter than the sprue, we can neglect the velocity at the surface of the pouring basin (v1 = 0) and use the formula for the area of a circle:
A = πr2
Substituting, we get:
π(0.0355 m)2v2 = π(r2)2 x 20
where r2 is the radius of the pouring basin.
Solving for v2, we get:
v2 = 20 x (0.0355/0.5)2 m/s
Finally, we can calculate the diameter of the sprue base using the formula for the velocity of a fluid through a pipe:
v = (2gh)1/2
where h is the height of the sprue.
Substituting, we get:
(20/7800) = (2 x 9.81 x 0.25 x π/4)1/2 x (π/4) x (d/100)2
Solving for d, we get:
d = 3.55 cm
Therefore, the diameter of the sprue base is 3.55 cm.
Given:
Rate of delivery of liquid iron = 20 kg/s
Density of iron = 7800 kg/m3
Height of pouring basin = 9 cm
Height of sprue = 25 cm
Let's calculate the pressure head of liquid iron in the sprue using Bernoulli's equation:
P1/ρg + v1^2/2g + h1 = P2/ρg + v2^2/2g + h2
where,
P1 = pressure at the surface of the liquid iron in the pouring basin (atmospheric pressure)
P2 = pressure at the base of the sprue (unknown)
ρ = density of liquid iron
g = acceleration due to gravity
v1 = velocity of liquid iron at the surface of the pouring basin (zero)
v2 = velocity of liquid iron at the base of the sprue (unknown)
h1 = height of the surface of the liquid iron above the base of the sprue (9 cm + 25 cm = 34 cm)
h2 = height of the base of the sprue above the surface of the liquid iron in the pouring basin (unknown)
Substituting the given values, we get:
P2/7800g + v2^2/2g + 0.34 m = Patm/7800g + 0
where Patm is atmospheric pressure.
Since the velocity of liquid iron at the base of the sprue is negligible compared to the velocity at the surface of the pouring basin, we can neglect the second term.
Solving for P2, we get:
P2 = (Patm + 7800g x 0.34) Pa
Next, we can calculate the velocity of liquid iron at the base of the sprue using the equation of continuity:
A1v1 = A2v2
where A1 and A2 are the cross-sectional areas of the pouring basin and sprue, respectively.
Assuming the pouring basin has a larger diameter than the sprue, we can neglect the velocity at the surface of the pouring basin (v1 = 0) and use the formula for the area of a circle:
A = πr2
Substituting, we get:
π(0.0355 m)2v2 = π(r2)2 x 20
where r2 is the radius of the pouring basin.
Solving for v2, we get:
v2 = 20 x (0.0355/0.5)2 m/s
Finally, we can calculate the diameter of the sprue base using the formula for the velocity of a fluid through a pipe:
v = (2gh)1/2
where h is the height of the sprue.
Substituting, we get:
(20/7800) = (2 x 9.81 x 0.25 x π/4)1/2 x (π/4) x (d/100)2
Solving for d, we get:
d = 3.55 cm
Therefore, the diameter of the sprue base is 3.55 cm.
Free Test
FREE
| Start Free Test |
Community Answer
A sprue for avoiding aspiration todeliver liquid iron at a rate of 20k...
We know, mass flow rate is density × area × velocity....(1) velocity is sq Root of 2gh. h is 34cm. area is π d sq/4 put all in the eq 1...you will get d as 3.55 cm
Attention Mechanical Engineering Students!
To make sure you are not studying endlessly, EduRev has designed Mechanical Engineering study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Mechanical Engineering.
|
Explore Courses for Mechanical Engineering exam
|
|
Similar Mechanical Engineering Doubts
Top Courses for Mechanical EngineeringView all
A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer?
Question Description
A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer?.
A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer?.
Solutions for A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A sprue for avoiding aspiration todeliver liquid iron at a rate of 20kg/s. The density of iron is 7800kg/m3. The height of pouring basinis 9cm. and height of sprue is 25cm.Diameter of sprue base is:-a)3.55 cmb)4.55 cmc)3.75 cmd)5.75 cmCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.
|
|
Explore Courses for Mechanical Engineering exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup