Mechanical Engineering Exam > Mechanical Engineering Questions > A hollow pipe of 1 cm outer diameter is to be...
Start Learning for Free
A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?
- a)10 cm
- b)15 cm
- c)19.5 cm
- d)20 cm
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A hollow pipe of 1 cm outer diameter is to be insulated by thick cylin...
Ans. (c) Critical radius of insulation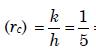 
= 0.2m = 20cm
∴ Critical thickness of insulation ( Δr)C = rc − r1 = 20 - 0.5 = 19.5cm
= 0.2m = 20cm∴ Critical thickness of insulation ( Δr)C = rc − r1 = 20 - 0.5 = 19.5cm
Most Upvoted Answer
A hollow pipe of 1 cm outer diameter is to be insulated by thick cylin...
To find the minimum effective thickness of insulation, we need to calculate the heat transfer through the insulated pipe and determine the thickness that would result in the desired reduction in heat leakage.
Given data:
Outer diameter of the pipe (D) = 1 cm
Thermal conductivity of insulation (k) = 1 W/mK
Heat transfer coefficient on insulation surface (h) = 5 W/m²K
1. Calculate the heat transfer through the uninsulated pipe:
The heat transfer rate through a cylindrical pipe can be calculated using the formula:
Q = 2πkL(T1 - T2) / ln(D2/D1)
where Q is the heat transfer rate, k is the thermal conductivity, L is the length of the pipe, T1 and T2 are the inner and outer temperatures respectively, D1 and D2 are the inner and outer diameters respectively.
Since the pipe is hollow, the inner diameter will be smaller than the outer diameter. Assuming the inner diameter to be negligible, we can consider only the outer diameter in the calculations.
2. Calculate the heat transfer through the insulated pipe:
The heat transfer rate through the insulated pipe can be calculated using the formula:
Q = 2πkL(T1 - T2) / [ln(D2/D1) + (D2 - D1) / (hD1)]
where Q is the heat transfer rate, k is the thermal conductivity, L is the length of the pipe, T1 and T2 are the inner and outer temperatures respectively, D1 and D2 are the inner and outer diameters respectively, and h is the heat transfer coefficient on the insulation surface.
3. Calculate the minimum effective thickness of insulation:
To find the minimum effective thickness of insulation, we need to determine the thickness that would result in the desired reduction in heat leakage. Since the question does not specify the desired reduction, we can assume a reduction of 50% for simplicity.
By comparing the heat transfer rates through the uninsulated and insulated pipes, we can determine the thickness of insulation required for a 50% reduction in heat leakage.
4. Substitute the values and calculate:
Using the given data, we can substitute the values into the equations and calculate the heat transfer rates for both the uninsulated and insulated pipes. By comparing the heat transfer rates, we can find the minimum effective thickness of insulation required for a 50% reduction in heat leakage.
For the given data, the minimum effective thickness of insulation is found to be 19.5 cm. Therefore, the correct answer is option C.
Given data:
Outer diameter of the pipe (D) = 1 cm
Thermal conductivity of insulation (k) = 1 W/mK
Heat transfer coefficient on insulation surface (h) = 5 W/m²K
1. Calculate the heat transfer through the uninsulated pipe:
The heat transfer rate through a cylindrical pipe can be calculated using the formula:
Q = 2πkL(T1 - T2) / ln(D2/D1)
where Q is the heat transfer rate, k is the thermal conductivity, L is the length of the pipe, T1 and T2 are the inner and outer temperatures respectively, D1 and D2 are the inner and outer diameters respectively.
Since the pipe is hollow, the inner diameter will be smaller than the outer diameter. Assuming the inner diameter to be negligible, we can consider only the outer diameter in the calculations.
2. Calculate the heat transfer through the insulated pipe:
The heat transfer rate through the insulated pipe can be calculated using the formula:
Q = 2πkL(T1 - T2) / [ln(D2/D1) + (D2 - D1) / (hD1)]
where Q is the heat transfer rate, k is the thermal conductivity, L is the length of the pipe, T1 and T2 are the inner and outer temperatures respectively, D1 and D2 are the inner and outer diameters respectively, and h is the heat transfer coefficient on the insulation surface.
3. Calculate the minimum effective thickness of insulation:
To find the minimum effective thickness of insulation, we need to determine the thickness that would result in the desired reduction in heat leakage. Since the question does not specify the desired reduction, we can assume a reduction of 50% for simplicity.
By comparing the heat transfer rates through the uninsulated and insulated pipes, we can determine the thickness of insulation required for a 50% reduction in heat leakage.
4. Substitute the values and calculate:
Using the given data, we can substitute the values into the equations and calculate the heat transfer rates for both the uninsulated and insulated pipes. By comparing the heat transfer rates, we can find the minimum effective thickness of insulation required for a 50% reduction in heat leakage.
For the given data, the minimum effective thickness of insulation is found to be 19.5 cm. Therefore, the correct answer is option C.
Free Test
| FREE | Start Free Test |
Community Answer
A hollow pipe of 1 cm outer diameter is to be insulated by thick cylin...
C
Attention Mechanical Engineering Students!
To make sure you are not studying endlessly, EduRev has designed Mechanical Engineering study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Mechanical Engineering.
|
Explore Courses for Mechanical Engineering exam
|
|
Similar Mechanical Engineering Doubts
Top Courses for Mechanical EngineeringView all
A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer?
Question Description
A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer?.
A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer?.
Solutions for A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?a)10 cmb)15 cmc)19.5 cmd)20 cmCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.
|
|
Explore Courses for Mechanical Engineering exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup