Class 12 Exam > Class 12 Questions > Derive the expression for drift velocity?
Start Learning for Free
Derive the expression for drift velocity?
Verified Answer
Derive the expression for drift velocity?
In physics a drift velocity is the average velocity attained by charged particles, such as electrons, in a material due to an electric field. In general, an electron in a conductor will propagate randomly at the Fermi velocity, resulting in an average velocity of zero. Applying an electric field adds to this random motion a small net flow in one direction; this is the drift.
Drift velocity is proportional to current. In a resistive material it is also proportional to the magnitude of an external electric field. Thus Ohm's law can be explained in terms of drift velocity. The law's most elementary expression is:
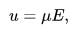
where u is drift velocity, μ is the material's electron mobility, and E is the electric field. In the MKS system these quantities' units are m/s, m^2/(V.s), and V/m, respectively.
When a potential difference is applied across a conductor, free electrons gain velocity in the direction opposite to the electric field between successive collisions, thus acquiring a velocity component in that direction in addition to its random thermal velocity. As a result there is a definite small drift velocity of electrons, which is superimposed on the random motion of free electrons. Due to this drift velocity, there is a net flow of electrons opposite to the direction of the field.
 This question is part of UPSC exam. View all Class 12 courses
This question is part of UPSC exam. View all Class 12 courses
Most Upvoted Answer
Derive the expression for drift velocity?
Drift Velocity:
Drift velocity refers to the average velocity at which charges (such as electrons or ions) move through a conductor in response to an electric field. It is an important concept in understanding the flow of current in a conductor. The expression for drift velocity can be derived using the concept of current density.
Current Density:
Current density is defined as the amount of current flowing per unit cross-sectional area of a conductor. It is denoted by the symbol J and is given by the equation:
J = I / A
where J is the current density, I is the current flowing through the conductor, and A is the cross-sectional area of the conductor.
Charge Carriers and Drift Velocity:
In a conductor, such as a metal wire, there are free charge carriers (electrons or ions) that can move. When an electric field is applied across the conductor, these charge carriers experience a force due to the field and start moving. However, due to the presence of collisions with the lattice structure of the conductor, their motion is not uniform.
Deriving the Expression:
To derive the expression for drift velocity, we consider the average velocity of the charge carriers. The average velocity can be defined as the total distance traveled divided by the total time taken. In the case of charge carriers, the total distance traveled is the length of the conductor, L, and the total time taken is the relaxation time, τ.
Therefore, the average velocity is given by:
v_avg = L / τ
The relaxation time, τ, represents the average time between successive collisions of charge carriers with the lattice structure. It depends on the material properties and temperature.
Relation between Current and Charge Carriers:
The current flowing through a conductor can be expressed as the product of charge carriers and their average velocity. Mathematically, it can be represented as:
I = n * q * A * v_avg
where n is the number density of charge carriers, q is the charge of a single carrier, A is the cross-sectional area of the conductor, and v_avg is the average velocity.
Expressing Drift Velocity:
From the above equations, we can express the drift velocity, v_d, as:
v_d = v_avg = I / (n * q * A)
This expression shows that the drift velocity is inversely proportional to the number density of charge carriers, the charge of a single carrier, and the cross-sectional area of the conductor. It is directly proportional to the current flowing through the conductor.
Conclusion:
In conclusion, the expression for drift velocity is derived by considering the average velocity of charge carriers in a conductor. It is an important parameter that describes the motion of charge carriers in response to an electric field. The expression for drift velocity provides insights into the relationship between current, charge carriers, and the properties of the conductor.
Drift velocity refers to the average velocity at which charges (such as electrons or ions) move through a conductor in response to an electric field. It is an important concept in understanding the flow of current in a conductor. The expression for drift velocity can be derived using the concept of current density.
Current Density:
Current density is defined as the amount of current flowing per unit cross-sectional area of a conductor. It is denoted by the symbol J and is given by the equation:
J = I / A
where J is the current density, I is the current flowing through the conductor, and A is the cross-sectional area of the conductor.
Charge Carriers and Drift Velocity:
In a conductor, such as a metal wire, there are free charge carriers (electrons or ions) that can move. When an electric field is applied across the conductor, these charge carriers experience a force due to the field and start moving. However, due to the presence of collisions with the lattice structure of the conductor, their motion is not uniform.
Deriving the Expression:
To derive the expression for drift velocity, we consider the average velocity of the charge carriers. The average velocity can be defined as the total distance traveled divided by the total time taken. In the case of charge carriers, the total distance traveled is the length of the conductor, L, and the total time taken is the relaxation time, τ.
Therefore, the average velocity is given by:
v_avg = L / τ
The relaxation time, τ, represents the average time between successive collisions of charge carriers with the lattice structure. It depends on the material properties and temperature.
Relation between Current and Charge Carriers:
The current flowing through a conductor can be expressed as the product of charge carriers and their average velocity. Mathematically, it can be represented as:
I = n * q * A * v_avg
where n is the number density of charge carriers, q is the charge of a single carrier, A is the cross-sectional area of the conductor, and v_avg is the average velocity.
Expressing Drift Velocity:
From the above equations, we can express the drift velocity, v_d, as:
v_d = v_avg = I / (n * q * A)
This expression shows that the drift velocity is inversely proportional to the number density of charge carriers, the charge of a single carrier, and the cross-sectional area of the conductor. It is directly proportional to the current flowing through the conductor.
Conclusion:
In conclusion, the expression for drift velocity is derived by considering the average velocity of charge carriers in a conductor. It is an important parameter that describes the motion of charge carriers in response to an electric field. The expression for drift velocity provides insights into the relationship between current, charge carriers, and the properties of the conductor.

|
Explore Courses for Class 12 exam
|

|
Derive the expression for drift velocity?
Question Description
Derive the expression for drift velocity? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Derive the expression for drift velocity? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Derive the expression for drift velocity?.
Derive the expression for drift velocity? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Derive the expression for drift velocity? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Derive the expression for drift velocity?.
Solutions for Derive the expression for drift velocity? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Derive the expression for drift velocity? defined & explained in the simplest way possible. Besides giving the explanation of
Derive the expression for drift velocity?, a detailed solution for Derive the expression for drift velocity? has been provided alongside types of Derive the expression for drift velocity? theory, EduRev gives you an
ample number of questions to practice Derive the expression for drift velocity? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

















