JEE Exam > JEE Questions > A spider and fly are on a glass sphere. as th...
Start Learning for Free
A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2?
Most Upvoted Answer
A spider and fly are on a glass sphere. as the fly moves on the surfac...
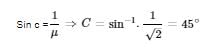
 \
\
Community Answer
A spider and fly are on a glass sphere. as the fly moves on the surfac...
Introduction:
The scenario involves a spider and a fly on the surface of a glass sphere. We need to determine the maximum area on the glass sphere from where the spider can see the fly. The radius of the sphere is assumed to be much larger than the size of the spider and the fly, and the refractive index of the glass is given as √2.
Explanation:
To understand how the spider can see the fly on the glass sphere, we need to consider the concept of refraction. Refraction occurs when light passes through different mediums, such as air and glass, and bends due to the change in the speed of light. In this case, the light from the fly will undergo refraction as it passes through the glass sphere.
1. Angle of Deviation:
The angle of deviation is the angle by which a ray of light is bent when it enters a different medium. It depends on the angle of incidence and the refractive indices of the mediums involved. In this case, the angle of deviation will determine the maximum area on the glass sphere from where the spider can see the fly.
2. Snell's Law:
Snell's law relates the angles of incidence and refraction, and the refractive indices of the two mediums. It is given by the equation: n1 * sin(θ1) = n2 * sin(θ2), where n1 and n2 are the refractive indices, and θ1 and θ2 are the angles of incidence and refraction, respectively.
3. Critical Angle:
The critical angle is the angle of incidence that results in an angle of refraction of 90 degrees. If the angle of incidence exceeds the critical angle, total internal reflection occurs, and the light is reflected back into the original medium. In this case, total internal reflection will prevent the spider from seeing the fly.
4. Calculating the Maximum Area:
To calculate the maximum area on the glass sphere, we need to find the critical angle. The critical angle can be determined using the refractive indices of air and glass. The refractive index of air is approximately 1, and the refractive index of glass is given as √2.
Using Snell's law, we can rearrange the equation to calculate the critical angle: critical angle = arcsin(n2/n1).
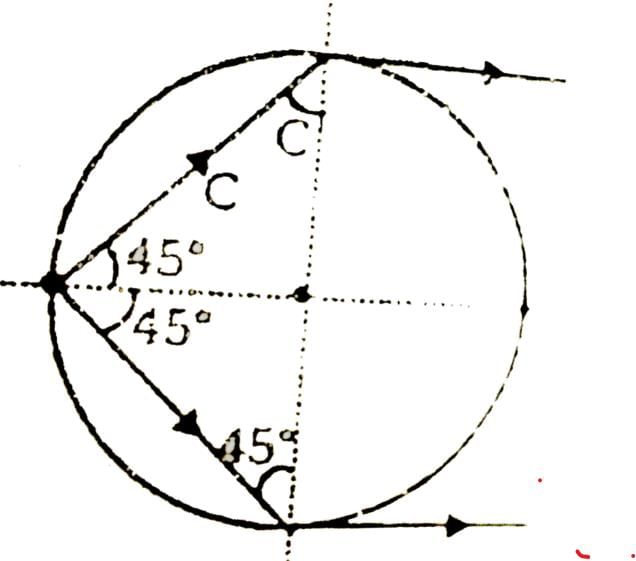
For the given scenario, the critical angle can be calculated as follows: critical angle = arcsin(√2/1) ≈ 54.74 degrees.
Considering the glass sphere, the spider will be able to see the fly within a cone-shaped region with the vertex at the center of the sphere. The maximum area on the glass sphere from where the spider can see the fly would be the curved surface area of this cone.
Conclusion:
In conclusion, the maximum area on the glass sphere from where the spider can see the fly is determined by the critical angle of refraction. By calculating the critical angle using the refractive indices of air and glass, we found that the maximum area is within a cone-shaped region on the glass sphere. This cone's curved surface area represents the maximum area from where the spider can see the fly.
The scenario involves a spider and a fly on the surface of a glass sphere. We need to determine the maximum area on the glass sphere from where the spider can see the fly. The radius of the sphere is assumed to be much larger than the size of the spider and the fly, and the refractive index of the glass is given as √2.
Explanation:
To understand how the spider can see the fly on the glass sphere, we need to consider the concept of refraction. Refraction occurs when light passes through different mediums, such as air and glass, and bends due to the change in the speed of light. In this case, the light from the fly will undergo refraction as it passes through the glass sphere.
1. Angle of Deviation:
The angle of deviation is the angle by which a ray of light is bent when it enters a different medium. It depends on the angle of incidence and the refractive indices of the mediums involved. In this case, the angle of deviation will determine the maximum area on the glass sphere from where the spider can see the fly.
2. Snell's Law:
Snell's law relates the angles of incidence and refraction, and the refractive indices of the two mediums. It is given by the equation: n1 * sin(θ1) = n2 * sin(θ2), where n1 and n2 are the refractive indices, and θ1 and θ2 are the angles of incidence and refraction, respectively.
3. Critical Angle:
The critical angle is the angle of incidence that results in an angle of refraction of 90 degrees. If the angle of incidence exceeds the critical angle, total internal reflection occurs, and the light is reflected back into the original medium. In this case, total internal reflection will prevent the spider from seeing the fly.
4. Calculating the Maximum Area:
To calculate the maximum area on the glass sphere, we need to find the critical angle. The critical angle can be determined using the refractive indices of air and glass. The refractive index of air is approximately 1, and the refractive index of glass is given as √2.
Using Snell's law, we can rearrange the equation to calculate the critical angle: critical angle = arcsin(n2/n1).
For the given scenario, the critical angle can be calculated as follows: critical angle = arcsin(√2/1) ≈ 54.74 degrees.
Considering the glass sphere, the spider will be able to see the fly within a cone-shaped region with the vertex at the center of the sphere. The maximum area on the glass sphere from where the spider can see the fly would be the curved surface area of this cone.
Conclusion:
In conclusion, the maximum area on the glass sphere from where the spider can see the fly is determined by the critical angle of refraction. By calculating the critical angle using the refractive indices of air and glass, we found that the maximum area is within a cone-shaped region on the glass sphere. This cone's curved surface area represents the maximum area from where the spider can see the fly.

|
Explore Courses for JEE exam
|

|
Similar JEE Doubts
A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2?
Question Description
A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2?.
A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2?.
Solutions for A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2? defined & explained in the simplest way possible. Besides giving the explanation of
A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2?, a detailed solution for A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2? has been provided alongside types of A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2? theory, EduRev gives you an
ample number of questions to practice A spider and fly are on a glass sphere. as the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it?assume that radius radius of sphere is much larger than size of spider and the fly. take a refactive index of glass equal to root2? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























