Class 11 Exam > Class 11 Questions > A neutron moving with a speed of 10^6 m/s suf...
Start Learning for Free
A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus?
Verified Answer
A neutron moving with a speed of 10^6 m/s suffers a head on collision ...
Here in this case let a neutron of mass m1 and initial speed u1 strikes a nucleus with mass m2 which is at rest so u2 = 0 and undergoes a perfectly elastic collision . Again let us consider that the final velocity of the neutron is v1.
Now from conservation of kinetic energy and conservation of momentum we can write that ,
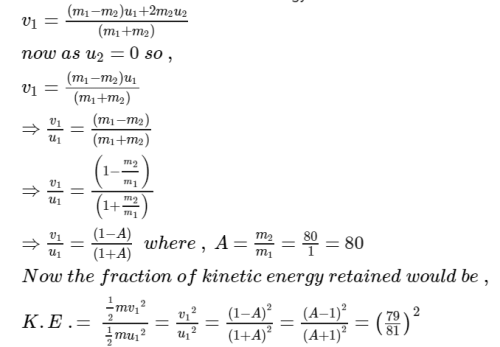
 This question is part of UPSC exam. View all Class 11 courses
This question is part of UPSC exam. View all Class 11 courses
Most Upvoted Answer
A neutron moving with a speed of 10^6 m/s suffers a head on collision ...
Head-on Collision of Neutron with Nucleus
In a head-on collision between a neutron and a nucleus, we need to determine the fraction of energy retained by the nucleus after the collision. To solve this problem, we can use the concept of conservation of momentum and conservation of energy.
Conservation of Momentum:
In a collision, the total momentum before the collision is equal to the total momentum after the collision, assuming no external forces are acting on the system.
Conservation of Energy:
In an ideal elastic collision, both momentum and kinetic energy are conserved. However, in a real-world scenario, there may be some energy losses due to various factors like deformation, heat, and sound generation.
Given Data:
- Speed of neutron (v) = 10^6 m/s
- Mass number of the nucleus (A) = 80
- Assume the initial velocity of the nucleus (V) is zero.
Calculating the Fraction of Energy Retained:
1. Calculate the initial momentum of the system.
- Momentum (p) = mass (m) × velocity (v)
- Momentum of neutron (p_neutron) = m_neutron × v_neutron
- Momentum of nucleus (p_nucleus) = m_nucleus × v_nucleus (initially zero)
- Total initial momentum (p_initial) = p_neutron + p_nucleus
2. Apply the conservation of momentum to find the final velocity of the nucleus.
- Momentum of the neutron after collision = -p_neutron (opposite direction)
- Momentum of the nucleus after collision = p_nucleus
- Total final momentum (p_final) = -p_neutron + p_nucleus
3. Calculate the final kinetic energy of the system.
- Kinetic energy (KE) = 0.5 × mass × velocity^2
- Initial kinetic energy (KE_initial) = 0.5 × m_neutron × v_neutron^2
- Final kinetic energy (KE_final) = 0.5 × m_neutron × (-v_neutron)^2 + 0.5 × m_nucleus × v_nucleus^2
4. Calculate the fraction of energy retained by the nucleus.
- Fraction of energy retained = (KE_final - KE_initial) / KE_initial
Explanation:
In a head-on collision, the neutron transfers some of its momentum and energy to the nucleus. The fraction of energy retained by the nucleus depends on the masses and velocities of both the neutron and the nucleus.
By applying the conservation of momentum, we can find the final velocity of the nucleus after the collision. Then, using the conservation of energy, we can calculate the final kinetic energy of the system. The difference between the initial and final kinetic energies gives us the energy lost during the collision.
The fraction of energy retained by the nucleus is obtained by dividing the energy lost by the initial kinetic energy. This fraction represents the efficiency of the collision in terms of energy transfer.
It's important to note that in real-world scenarios, collisions are not perfectly elastic, and some energy is always lost due to various factors such as deformation, heat generation, and sound production.
In a head-on collision between a neutron and a nucleus, we need to determine the fraction of energy retained by the nucleus after the collision. To solve this problem, we can use the concept of conservation of momentum and conservation of energy.
Conservation of Momentum:
In a collision, the total momentum before the collision is equal to the total momentum after the collision, assuming no external forces are acting on the system.
Conservation of Energy:
In an ideal elastic collision, both momentum and kinetic energy are conserved. However, in a real-world scenario, there may be some energy losses due to various factors like deformation, heat, and sound generation.
Given Data:
- Speed of neutron (v) = 10^6 m/s
- Mass number of the nucleus (A) = 80
- Assume the initial velocity of the nucleus (V) is zero.
Calculating the Fraction of Energy Retained:
1. Calculate the initial momentum of the system.
- Momentum (p) = mass (m) × velocity (v)
- Momentum of neutron (p_neutron) = m_neutron × v_neutron
- Momentum of nucleus (p_nucleus) = m_nucleus × v_nucleus (initially zero)
- Total initial momentum (p_initial) = p_neutron + p_nucleus
2. Apply the conservation of momentum to find the final velocity of the nucleus.
- Momentum of the neutron after collision = -p_neutron (opposite direction)
- Momentum of the nucleus after collision = p_nucleus
- Total final momentum (p_final) = -p_neutron + p_nucleus
3. Calculate the final kinetic energy of the system.
- Kinetic energy (KE) = 0.5 × mass × velocity^2
- Initial kinetic energy (KE_initial) = 0.5 × m_neutron × v_neutron^2
- Final kinetic energy (KE_final) = 0.5 × m_neutron × (-v_neutron)^2 + 0.5 × m_nucleus × v_nucleus^2
4. Calculate the fraction of energy retained by the nucleus.
- Fraction of energy retained = (KE_final - KE_initial) / KE_initial
Explanation:
In a head-on collision, the neutron transfers some of its momentum and energy to the nucleus. The fraction of energy retained by the nucleus depends on the masses and velocities of both the neutron and the nucleus.
By applying the conservation of momentum, we can find the final velocity of the nucleus after the collision. Then, using the conservation of energy, we can calculate the final kinetic energy of the system. The difference between the initial and final kinetic energies gives us the energy lost during the collision.
The fraction of energy retained by the nucleus is obtained by dividing the energy lost by the initial kinetic energy. This fraction represents the efficiency of the collision in terms of energy transfer.
It's important to note that in real-world scenarios, collisions are not perfectly elastic, and some energy is always lost due to various factors such as deformation, heat generation, and sound production.
Attention Class 11 Students!
To make sure you are not studying endlessly, EduRev has designed Class 11 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 11.

|
Explore Courses for Class 11 exam
|

|
A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus?
Question Description
A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus?.
A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus?.
Solutions for A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus? defined & explained in the simplest way possible. Besides giving the explanation of
A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus?, a detailed solution for A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus? has been provided alongside types of A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus? theory, EduRev gives you an
ample number of questions to practice A neutron moving with a speed of 10^6 m/s suffers a head on collision with a nucleus of mass number 80. What is the friction of energy retained by the nucleus? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























