Class 11 Exam > Class 11 Questions > A block slides down on a inclined plane of sl...
Start Learning for Free
A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ?
Verified Answer
A block slides down on a inclined plane of slope angle theta with cons...
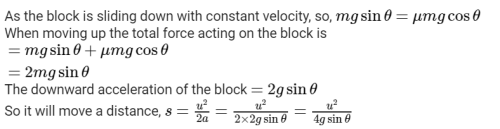
 This question is part of UPSC exam. View all Class 11 courses
This question is part of UPSC exam. View all Class 11 courses
Most Upvoted Answer
A block slides down on a inclined plane of slope angle theta with cons...
Introduction:
When a block slides down an inclined plane with a constant velocity and is then projected on the same plane with an initial velocity, it eventually comes to rest at a certain distance along the incline. In this explanation, we will determine how far the block will move before coming to rest.
Analysis:
To solve this problem, we need to consider the forces acting on the block and apply the principles of motion. Let's break down the analysis into the following key points:
1. Forces:
- Gravity force acts vertically downwards and can be resolved into two components: one parallel to the incline (mg sinθ) and the other perpendicular to the incline (mg cosθ).
- The normal force acts perpendicular to the incline and counterbalances the component of gravity perpendicular to the incline, i.e., mg cosθ.
- The frictional force acts parallel to the incline and opposes the motion of the block.
2. Sliding Down the Incline:
When the block slides down the inclined plane with a constant velocity, the frictional force exactly balances the component of gravity parallel to the incline. Therefore, the frictional force is given by:
Frictional force, f = mg sinθ
3. Projecting on the Incline:
When the block is projected on the incline with an initial velocity, it initially experiences an additional force due to the projection. This force is parallel to the incline and reduces with time until it becomes zero.
4. Coming to Rest:
To determine the distance the block will move before coming to rest, we need to find the point where the frictional force becomes zero. At this point, the net force acting on the block will be zero, causing it to come to rest.
5. Equilibrium Condition:
The net force on the block can be expressed as the difference between the component of the initial velocity parallel to the incline and the frictional force:
Net force = mg sinθ - μmg cosθ
where μ is the coefficient of friction.
6. Distance Calculation:
Equating the net force to zero, we can solve for the distance x:
mg sinθ - μmg cosθ = 0
μmg cosθ = mg sinθ
μ = tanθ
Therefore, the distance moved by the block before coming to rest is given by:
x = u² / (2g tanθ)
Conclusion:
In conclusion, the block will move a distance of u² / (2g tanθ) along the inclined plane before coming to rest. The analysis considered the forces acting on the block, the equilibrium condition, and the principles of motion to determine the distance.
When a block slides down an inclined plane with a constant velocity and is then projected on the same plane with an initial velocity, it eventually comes to rest at a certain distance along the incline. In this explanation, we will determine how far the block will move before coming to rest.
Analysis:
To solve this problem, we need to consider the forces acting on the block and apply the principles of motion. Let's break down the analysis into the following key points:
1. Forces:
- Gravity force acts vertically downwards and can be resolved into two components: one parallel to the incline (mg sinθ) and the other perpendicular to the incline (mg cosθ).
- The normal force acts perpendicular to the incline and counterbalances the component of gravity perpendicular to the incline, i.e., mg cosθ.
- The frictional force acts parallel to the incline and opposes the motion of the block.
2. Sliding Down the Incline:
When the block slides down the inclined plane with a constant velocity, the frictional force exactly balances the component of gravity parallel to the incline. Therefore, the frictional force is given by:
Frictional force, f = mg sinθ
3. Projecting on the Incline:
When the block is projected on the incline with an initial velocity, it initially experiences an additional force due to the projection. This force is parallel to the incline and reduces with time until it becomes zero.
4. Coming to Rest:
To determine the distance the block will move before coming to rest, we need to find the point where the frictional force becomes zero. At this point, the net force acting on the block will be zero, causing it to come to rest.
5. Equilibrium Condition:
The net force on the block can be expressed as the difference between the component of the initial velocity parallel to the incline and the frictional force:
Net force = mg sinθ - μmg cosθ
where μ is the coefficient of friction.
6. Distance Calculation:
Equating the net force to zero, we can solve for the distance x:
mg sinθ - μmg cosθ = 0
μmg cosθ = mg sinθ
μ = tanθ
Therefore, the distance moved by the block before coming to rest is given by:
x = u² / (2g tanθ)
Conclusion:
In conclusion, the block will move a distance of u² / (2g tanθ) along the inclined plane before coming to rest. The analysis considered the forces acting on the block, the equilibrium condition, and the principles of motion to determine the distance.
Community Answer
A block slides down on a inclined plane of slope angle theta with cons...
V^2/2g
Attention Class 11 Students!
To make sure you are not studying endlessly, EduRev has designed Class 11 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 11.

|
Explore Courses for Class 11 exam
|

|
Similar Class 11 Doubts
A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ?
Question Description
A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ?.
A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ?.
Solutions for A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ? defined & explained in the simplest way possible. Besides giving the explanation of
A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ?, a detailed solution for A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ? has been provided alongside types of A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ? theory, EduRev gives you an
ample number of questions to practice A block slides down on a inclined plane of slope angle theta with constant velocity. It is then projected on same plane with initial velocity u. How far the incline will it move before coming to rest. ? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.




















