Class 9 Exam > Class 9 Questions > Prove that an isosceles trapezium is always c...
Start Learning for Free
Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ?
Verified Answer
Prove that an isosceles trapezium is always cyclic and it's diagonal a...
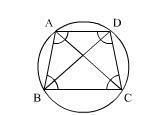
In a cyclic trapezium,
∠BAD + ∠BCD = 180degree
∠BAD + ∠ABC = 180degree
∴ ∠ABC = ∠BCD
In ∆ABC and ∆BDC,
⇒∠ABC = ∠BCD
⇒∠BAC = ∠CDB (angles in the same segment)
⇒BC = BC (common side)
⇒∆ABC ≅ ∆BDC
∴ AB = CD and AC = BD
Hence, cyclic trapezium ABCD is isosceles and diagonals are equal to each other.

 This question is part of UPSC exam. View all Class 9 courses
This question is part of UPSC exam. View all Class 9 courses
Most Upvoted Answer
Prove that an isosceles trapezium is always cyclic and it's diagonal a...
Proof that an isosceles trapezium is always cyclic and its diagonals are equal:
An isosceles trapezium is a quadrilateral with two parallel sides and two non-parallel sides, where the non-parallel sides are equal in length. In this proof, we will show that an isosceles trapezium is always cyclic, meaning that all four of its vertices lie on a common circle. Additionally, we will demonstrate that the diagonals of an isosceles trapezium are equal in length.
Proof:
1. Construct the trapezium:
Start by constructing an isosceles trapezium ABCD, where AB and CD are parallel sides, and AD = BC.
2. Extend the sides:
Extend the non-parallel sides AD and BC to meet at a point E.
3. Observe the triangles:
Notice that triangles ABE and CDE are congruent by the side-side-side (SSS) congruence criterion, as AB = CD (given), AD = BC (definition of an isosceles trapezium), and AE = CE (both are extensions of the parallel sides).
4. Prove the angles:
Since triangles ABE and CDE are congruent, their corresponding angles are also equal. Therefore, angle AEB = angle CED.
5. Prove the cyclic property:
Using the property that opposite angles in a cyclic quadrilateral are supplementary, we can conclude that angle AED + angle BEC = 180 degrees.
6. Prove the diagonals are equal:
Since opposite angles in a cyclic quadrilateral are supplementary, we have angle AED + angle BEC = 180 degrees. This implies that angle AED = angle BEC.
7. Observe the triangles again:
Notice that triangles ADE and BCE are congruent by the angle-side-angle (ASA) congruence criterion. Angle AED = angle BEC (proved in the previous step), AD = BC (definition of an isosceles trapezium), and AE = CE (both are extensions of the parallel sides).
8. Prove the length of diagonals:
Since triangles ADE and BCE are congruent, their corresponding sides are also equal. Therefore, DE = BE.
9. Conclude:
We have shown that an isosceles trapezium ABCD is cyclic because its opposite angles are supplementary. Additionally, the diagonals AD and BC are equal in length as proved by the congruence of triangles ADE and BCE.
Therefore, an isosceles trapezium is always cyclic, and its diagonals are equal in length.
An isosceles trapezium is a quadrilateral with two parallel sides and two non-parallel sides, where the non-parallel sides are equal in length. In this proof, we will show that an isosceles trapezium is always cyclic, meaning that all four of its vertices lie on a common circle. Additionally, we will demonstrate that the diagonals of an isosceles trapezium are equal in length.
Proof:
1. Construct the trapezium:
Start by constructing an isosceles trapezium ABCD, where AB and CD are parallel sides, and AD = BC.
2. Extend the sides:
Extend the non-parallel sides AD and BC to meet at a point E.
3. Observe the triangles:
Notice that triangles ABE and CDE are congruent by the side-side-side (SSS) congruence criterion, as AB = CD (given), AD = BC (definition of an isosceles trapezium), and AE = CE (both are extensions of the parallel sides).
4. Prove the angles:
Since triangles ABE and CDE are congruent, their corresponding angles are also equal. Therefore, angle AEB = angle CED.
5. Prove the cyclic property:
Using the property that opposite angles in a cyclic quadrilateral are supplementary, we can conclude that angle AED + angle BEC = 180 degrees.
6. Prove the diagonals are equal:
Since opposite angles in a cyclic quadrilateral are supplementary, we have angle AED + angle BEC = 180 degrees. This implies that angle AED = angle BEC.
7. Observe the triangles again:
Notice that triangles ADE and BCE are congruent by the angle-side-angle (ASA) congruence criterion. Angle AED = angle BEC (proved in the previous step), AD = BC (definition of an isosceles trapezium), and AE = CE (both are extensions of the parallel sides).
8. Prove the length of diagonals:
Since triangles ADE and BCE are congruent, their corresponding sides are also equal. Therefore, DE = BE.
9. Conclude:
We have shown that an isosceles trapezium ABCD is cyclic because its opposite angles are supplementary. Additionally, the diagonals AD and BC are equal in length as proved by the congruence of triangles ADE and BCE.
Therefore, an isosceles trapezium is always cyclic, and its diagonals are equal in length.
Attention Class 9 Students!
To make sure you are not studying endlessly, EduRev has designed Class 9 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 9.

|
Explore Courses for Class 9 exam
|

|
Similar Class 9 Doubts
Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ?
Question Description
Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ?.
Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ?.
Solutions for Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ? defined & explained in the simplest way possible. Besides giving the explanation of
Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ?, a detailed solution for Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ? has been provided alongside types of Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ? theory, EduRev gives you an
ample number of questions to practice Prove that an isosceles trapezium is always cyclic and it's diagonal are equal ? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























